Products of graphs¶
This module gathers everything related to graph products. At the moment it contains an implementation of a recognition algorithm for graphs that can be written as a Cartesian product of smaller ones.
Author:
Nathann Cohen (May 2012 – coded while watching the election of Francois Hollande on TV)
Cartesian product of graphs – the recognition problem¶
First, a definition:
Definition The Cartesian product of two graphs \(G\) and \(H\), denoted \(G\square H\), is a graph defined on the pairs \((g, h)\in V(G)\times V(H)\).
Two elements \((g, h),(g', h')\in V(G\square H)\) are adjacent in \(G\square H\) if and only if :
\(g=g'\) and \(hh'\in H\); or
\(h=h'\) and \(gg'\in G\)
Two remarks follow :
The Cartesian product is commutative
Any edge \(uv\) of a graph \(G_1 \square \cdots \square G_k\) can be given a color \(i\) corresponding to the unique index \(i\) such that \(u_i\) and \(v_i\) differ.
The problem that is of interest to us in the present module is the following:
Recognition problem Given a graph \(G\), can we guess whether there exist graphs \(G_1, ..., G_k\) such that \(G=G_1\square \cdots \square G_k\) ?
This problem can actually be solved, and the resulting factorization is unique. What is explained below can be found in the book Handbook of Product Graphs [HIK2011].
Everything is actually based on simple observations. Given a graph \(G\), finding out whether \(G\) can be written as the product of several graphs can be attempted by trying to color its edges according to some rules. Indeed, if we are to color the edges of \(G\) in such a way that each color class represents a factor of \(G\), we must ensure several things.
Remark 1 In any cycle of \(G\) no color can appear exactly once.
Indeed, if only one edge \(uv\) of a cycle were labelled with color \(i\), it would mean that:
The only difference between \(u\) and \(v\) lies in their \(i\) th coordinate
It is possible to go from \(u\) to \(v\) by changing only coordinates different from the \(i\) th
A contradiction indeed.

That means that, for instance, the edges of a triangle necessarily have the same color.
Remark 2 If two consecutive edges \(u_1u_2\) and \(u_2u_3\) have different colors, there necessarily exists a unique vertex \(u_4\) different from \(u_2\) and incident to both \(u_1\) and \(u_3\).
In this situation, opposed edges necessarily have the same colors because of the previous remark.
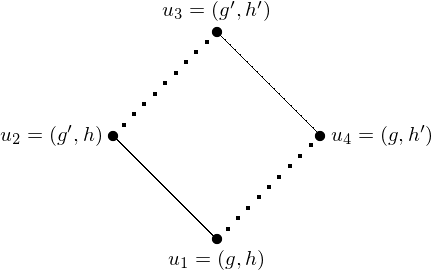
1st criterion : As a corollary, we know that:
If two vertices \(u,v\) have a unique common neighbor \(x\), then \(ux\) and \(xv\) have the same color.
If two vertices \(u, v\) have more that two common neighbors \(x_1, ..., x_k\) then all edges between the \(x_i\) and the vertices of \(u,v\) have the same color. This is also a consequence of the first remark.
2nd criterion : if two edges \(uv\) and \(u'v'\) of the product graph \(G\square H\) are such that \(d(u,u')+d(v,v')\neq d(u,v') + d(v,u')\) then the two edges \(uv\) and \(u'v'\) necessarily have the same color.
This is a consequence of the fact that for any two vertices \(u,v\) of \(G\square H\) (where \(u=(u_G,u_H)\) and \(v=(v_G,v_H)\)), we have \(d(u,v) = d_G(u_G,v_G)+d_H(u_H,v_H)\). Indeed, a shortest path from \(u\) to \(v\) in \(G\square H\) contains the information of a shortest path from \(u_G\) to \(v_G\) in \(G\), and a shortest path from \(u_H\) to \(v_H\) in \(H\).
The algorithm¶
The previous remarks tell us that some edges are in some way equivalent to some others, i.e. that their colors are equal. In order to compute the coloring we are looking for, we therefore build a graph on the edges of a graph \(G\), linking two edges whenever they are found to be equivalent according to the previous remarks.
All that is left to do is to compute the connected components of this new graph, as each of them representing the edges of a factor. Of course, only one connected component indicates that the graph has no factorization.
Then again, please refer to [HIK2011] for any technical question.
To Do¶
This implementation is made at Python level, and some parts of the algorithm
could be rewritten in Cython to save time. Especially when enumerating all pairs
of edges and computing their distances. This can easily be done in C with the
functions from the sage.graphs.distances_all_pairs module.
Methods¶
- sage.graphs.graph_decompositions.graph_products.is_cartesian_product(g, certificate=False, relabeling=False)[source]¶
Test whether the graph is a Cartesian product.
INPUT:
certificate– boolean (default:False); ifcertificate = False(default) the method only returnsTrueorFalseanswers. Ifcertificate = True, theTrueanswers are replaced by the list of the factors of the graph.relabeling– boolean (default:False); ifrelabeling = True(impliescertificate = True), the method also returns a dictionary associating to each vertex its natural coordinates as a vertex of a product graph. If \(g\) is not a Cartesian product,Noneis returned instead.
See also
graph_products– a module on graph products
Note
This algorithm may run faster whenever the graph’s vertices are integers (see
relabel()). Give it a try if it is too slow !EXAMPLES:
The Petersen graph is prime:
sage: from sage.graphs.graph_decompositions.graph_products import is_cartesian_product sage: g = graphs.PetersenGraph() sage: is_cartesian_product(g) False
>>> from sage.all import * >>> from sage.graphs.graph_decompositions.graph_products import is_cartesian_product >>> g = graphs.PetersenGraph() >>> is_cartesian_product(g) False
A 2d grid is the product of paths:
sage: g = graphs.Grid2dGraph(5,5) sage: p1, p2 = is_cartesian_product(g, certificate = True) sage: p1.is_isomorphic(graphs.PathGraph(5)) True sage: p2.is_isomorphic(graphs.PathGraph(5)) True
>>> from sage.all import * >>> g = graphs.Grid2dGraph(Integer(5),Integer(5)) >>> p1, p2 = is_cartesian_product(g, certificate = True) >>> p1.is_isomorphic(graphs.PathGraph(Integer(5))) True >>> p2.is_isomorphic(graphs.PathGraph(Integer(5))) True
Forgetting the graph’s labels, then finding them back:
sage: g.relabel() sage: b,D = g.is_cartesian_product(g, relabeling=True) sage: b True sage: D # random isomorphism {0: (20, 0), 1: (20, 1), 2: (20, 2), 3: (20, 3), 4: (20, 4), 5: (15, 0), 6: (15, 1), 7: (15, 2), 8: (15, 3), 9: (15, 4), 10: (10, 0), 11: (10, 1), 12: (10, 2), 13: (10, 3), 14: (10, 4), 15: (5, 0), 16: (5, 1), 17: (5, 2), 18: (5, 3), 19: (5, 4), 20: (0, 0), 21: (0, 1), 22: (0, 2), 23: (0, 3), 24: (0, 4)}
>>> from sage.all import * >>> g.relabel() >>> b,D = g.is_cartesian_product(g, relabeling=True) >>> b True >>> D # random isomorphism {0: (20, 0), 1: (20, 1), 2: (20, 2), 3: (20, 3), 4: (20, 4), 5: (15, 0), 6: (15, 1), 7: (15, 2), 8: (15, 3), 9: (15, 4), 10: (10, 0), 11: (10, 1), 12: (10, 2), 13: (10, 3), 14: (10, 4), 15: (5, 0), 16: (5, 1), 17: (5, 2), 18: (5, 3), 19: (5, 4), 20: (0, 0), 21: (0, 1), 22: (0, 2), 23: (0, 3), 24: (0, 4)}
And of course, we find the factors back when we build a graph from a product:
sage: g = graphs.PetersenGraph().cartesian_product(graphs.CycleGraph(3)) sage: g1, g2 = is_cartesian_product(g, certificate = True) sage: any( x.is_isomorphic(graphs.PetersenGraph()) for x in [g1,g2]) True sage: any( x.is_isomorphic(graphs.CycleGraph(3)) for x in [g1,g2]) True
>>> from sage.all import * >>> g = graphs.PetersenGraph().cartesian_product(graphs.CycleGraph(Integer(3))) >>> g1, g2 = is_cartesian_product(g, certificate = True) >>> any( x.is_isomorphic(graphs.PetersenGraph()) for x in [g1,g2]) True >>> any( x.is_isomorphic(graphs.CycleGraph(Integer(3))) for x in [g1,g2]) True
- sage.graphs.graph_decompositions.graph_products.rooted_product(G, H, root=None)[source]¶
Return the rooted product of \(G\) and \(H\).
The rooted product of two graphs \(G\) and \(H\) is the graph \(R\) defined as follows: take a copy of \(G\) and \(|V(G)|\) copies of \(H\), and for every vertex \(g_i\) of \(G\), identify \(g_i\) with the root of the \(i\)-th copy of \(H\). Mode formally, let \(V(G) = \{g_1, g_2, \ldots, g_n\}\), \(V(H) = \{h_1, h_2, \ldots, h_m\}\), and let \(h_1\) be the root vertex of \(H\). The vertex set \(V(R)\) is equal to the cartesian product of the sets of vertices \(V(G)\) and \(V(H)\), that is \(V(R) = \{(g_i, h_j) : g_i \in V(G), h_j \in V(H)\}\). The edge set \(E(R)\) is the union of the edges of a copy of \(G\), that is \(\{((g_i, h_1), (g_j, h_1)) : (g_i, g_j) \in E(G)\}\), and the edges of the copies of \(H\) for every \(g_i \in V(G)\), that is \(\{((g_i, h_j), (g_i, h_k)) : (h_j, h_k) \in V(H)\}\).
See Wikipedia article Rooted_product_of_graphs for more details.
See also
cartesian_product()– return the cartesian product of two graphsgraph_products– a module on graph products
EXAMPLES:
The rooted product of two trees is a tree:
sage: T1 = graphs.RandomTree(7) sage: T2 = graphs.RandomTree(8) sage: T = T1.rooted_product(T2) sage: T.is_tree() True
>>> from sage.all import * >>> T1 = graphs.RandomTree(Integer(7)) >>> T2 = graphs.RandomTree(Integer(8)) >>> T = T1.rooted_product(T2) >>> T.is_tree() True
The rooted product of \(G\) and \(H\) depends on the selected root in \(H\):
sage: G = graphs.CycleGraph(4) sage: H = graphs.PathGraph(3) sage: R1 = G.rooted_product(H, root=0) sage: R2 = G.rooted_product(H, root=1) sage: R1.is_isomorphic(R2) False sage: sorted(R1.degree()) [1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3] sage: sorted(R2.degree()) [1, 1, 1, 1, 1, 1, 1, 1, 4, 4, 4, 4]
>>> from sage.all import * >>> G = graphs.CycleGraph(Integer(4)) >>> H = graphs.PathGraph(Integer(3)) >>> R1 = G.rooted_product(H, root=Integer(0)) >>> R2 = G.rooted_product(H, root=Integer(1)) >>> R1.is_isomorphic(R2) False >>> sorted(R1.degree()) [1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3] >>> sorted(R2.degree()) [1, 1, 1, 1, 1, 1, 1, 1, 4, 4, 4, 4]
The domination number of the rooted product of any graph \(G\) and a path of order 2 is the order of \(G\):
sage: G = graphs.RandomGNP(20, .3) sage: P = graphs.PathGraph(2) sage: R = G.rooted_product(P) sage: len(R.dominating_set()) == G.order() # needs sage.numerical.mip True sage: G = digraphs.RandomDirectedGNP(20, .3) sage: P = digraphs.Path(2) sage: R = G.rooted_product(P) sage: len(R.dominating_set()) == G.order() # needs sage.numerical.mip True
>>> from sage.all import * >>> G = graphs.RandomGNP(Integer(20), RealNumber('.3')) >>> P = graphs.PathGraph(Integer(2)) >>> R = G.rooted_product(P) >>> len(R.dominating_set()) == G.order() # needs sage.numerical.mip True >>> G = digraphs.RandomDirectedGNP(Integer(20), RealNumber('.3')) >>> P = digraphs.Path(Integer(2)) >>> R = G.rooted_product(P) >>> len(R.dominating_set()) == G.order() # needs sage.numerical.mip True
The rooted product of two graphs is a subgraph of the cartesian product of the same two graphs:
sage: G = graphs.RandomGNP(6, .4) sage: H = graphs.RandomGNP(7, .4) sage: R = G.rooted_product(H) sage: C = G.cartesian_product(H) sage: R.is_subgraph(C, induced=False) True
>>> from sage.all import * >>> G = graphs.RandomGNP(Integer(6), RealNumber('.4')) >>> H = graphs.RandomGNP(Integer(7), RealNumber('.4')) >>> R = G.rooted_product(H) >>> C = G.cartesian_product(H) >>> R.is_subgraph(C, induced=False) True
Corner cases:
sage: Graph().rooted_product(Graph()) Rooted product of Graph on 0 vertices and Graph on 0 vertices: Graph on 0 vertices sage: Graph(1).rooted_product(Graph()) Rooted product of Graph on 1 vertex and Graph on 0 vertices: Graph on 0 vertices sage: Graph().rooted_product(Graph(1)) Rooted product of Graph on 0 vertices and Graph on 1 vertex: Graph on 0 vertices sage: Graph(1).rooted_product(Graph(1)) Rooted product of Graph on 1 vertex and Graph on 1 vertex: Graph on 1 vertex
>>> from sage.all import * >>> Graph().rooted_product(Graph()) Rooted product of Graph on 0 vertices and Graph on 0 vertices: Graph on 0 vertices >>> Graph(Integer(1)).rooted_product(Graph()) Rooted product of Graph on 1 vertex and Graph on 0 vertices: Graph on 0 vertices >>> Graph().rooted_product(Graph(Integer(1))) Rooted product of Graph on 0 vertices and Graph on 1 vertex: Graph on 0 vertices >>> Graph(Integer(1)).rooted_product(Graph(Integer(1))) Rooted product of Graph on 1 vertex and Graph on 1 vertex: Graph on 1 vertex