Parallel computations using RecursivelyEnumeratedSet and Map-Reduce#

There is an efficient way to distribute computations on a set \(S\) of objects defined by RecursivelyEnumeratedSet() (see sage.sets.recursively_enumerated_set for more details) over which one would like to perform the following kind of operations:

Compute the cardinality of a (very large) set defined recursively (through a call to RecursivelyEnumeratedSet_forest)
More generally, compute any kind of generating series over this set
Test a conjecture, e.g. find an element of \(S\) satisfying a specific property, or check that none does or that they all do
Count/list the elements of \(S\) that have a specific property
Apply any map/reduce kind of operation over the elements of \(S\)

AUTHORS:

Florent Hivert – code, documentation (2012–2016)
Jean Baptiste Priez – prototype, debugging help on MacOSX (2011-June, 2016)
Nathann Cohen – some documentation (2012)

How is this different from usual MapReduce?#

This implementation is specific to RecursivelyEnumeratedSet_forest, and uses its properties to do its job. Not only mapping and reducing but also generating the elements of \(S\) is done on different processors.

Advanced use#

Fine control over the execution of a map/reduce computation is achieved via parameters passed to the RESetMapReduce.run() method. The following three parameters can be used:

max_proc – (integer, default: None) if given, the maximum number of worker processors to use. The actual number is also bounded by the value of the environment variable SAGE_NUM_THREADS (the number of cores by default).
timeout – a timeout on the computation (default: None)
reduce_locally – whether the workers should reduce locally their work or sends results to the master as soon as possible. See RESetMapReduceWorker for details.

Here is an example or how to deal with timeout:

Sage

sage: from sage.parallel.map_reduce import (RESetMPExample, AbortError)
sage: EX = RESetMPExample(maxl=100)
sage: try:
....:     res = EX.run(timeout=float(0.01))
....: except AbortError:
....:     print("Computation timeout")
....: else:
....:     print("Computation normally finished")
....:     res
Computation timeout

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import (RESetMPExample, AbortError)
>>> EX = RESetMPExample(maxl=Integer(100))
>>> try:
...     res = EX.run(timeout=float(RealNumber('0.01')))
... except AbortError:
...     print("Computation timeout")
... else:
...     print("Computation normally finished")
...     res
Computation timeout

The following should not timeout even on a very slow machine:

Sage

sage: EX = RESetMPExample(maxl=8)
sage: try:
....:     res = EX.run(timeout=60)
....: except AbortError:
....:     print("Computation Timeout")
....: else:
....:     print("Computation normally finished")
....:     res
Computation normally finished
40320*x^8 + 5040*x^7 + 720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

Python

>>> from sage.all import *
>>> EX = RESetMPExample(maxl=Integer(8))
>>> try:
...     res = EX.run(timeout=Integer(60))
... except AbortError:
...     print("Computation Timeout")
... else:
...     print("Computation normally finished")
...     res
Computation normally finished
40320*x^8 + 5040*x^7 + 720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

As for reduce_locally, one should not see any difference, except for speed during normal usage. Most of the time one should leave it set to True, unless one sets up a mechanism to consume the partial results as soon as they arrive. See RESetParallelIterator and in particular the __iter__ method for a example of consumer use.

Profiling#

It is possible to profile a map/reduce computation. First we create a RESetMapReduce object:

Sage

sage: from sage.parallel.map_reduce import RESetMapReduce
sage: S = RESetMapReduce(
....:     roots=[[]],
....:     children=lambda l: [l + [0], l + [1]] if len(l) < 16 else [],
....:     map_function=lambda x: 1,
....:     reduce_function=lambda x, y: x + y,
....:     reduce_init=0)

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMapReduce
>>> S = RESetMapReduce(
...     roots=[[]],
...     children=lambda l: [l + [Integer(0)], l + [Integer(1)]] if len(l) < Integer(16) else [],
...     map_function=lambda x: Integer(1),
...     reduce_function=lambda x, y: x + y,
...     reduce_init=Integer(0))

The profiling is activated by the profile parameter. The value provided should be a prefix (including a possible directory) for the profile dump:

Sage

sage: import tempfile
sage: d = tempfile.TemporaryDirectory(prefix="RESetMR_profile")
sage: res = S.run(profile=d.name)  # random
[RESetMapReduceWorker-1:58] (20:00:41.444) Profiling in
/home/user/.sage/temp/.../32414/RESetMR_profilewRCRAx/profcomp1
...
[RESetMapReduceWorker-1:57] (20:00:41.444) Profiling in
/home/user/.sage/temp/.../32414/RESetMR_profilewRCRAx/profcomp0
...
sage: res
131071

Python

>>> from sage.all import *
>>> import tempfile
>>> d = tempfile.TemporaryDirectory(prefix="RESetMR_profile")
>>> res = S.run(profile=d.name)  # random
[RESetMapReduceWorker-1:58] (20:00:41.444) Profiling in
/home/user/.sage/temp/.../32414/RESetMR_profilewRCRAx/profcomp1
...
[RESetMapReduceWorker-1:57] (20:00:41.444) Profiling in
/home/user/.sage/temp/.../32414/RESetMR_profilewRCRAx/profcomp0
...
>>> res
131071

In this example, the profiles have been dumped in files such as profcomp0. One can then load and print them as follows. See cProfile.Profile for more details:

Sage

sage: import cProfile, pstats
sage: st = pstats.Stats(d.name+'0')
sage: st.strip_dirs().sort_stats('cumulative').print_stats()  # random
...
   Ordered by: cumulative time

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.023    0.023    0.432    0.432 map_reduce.py:1211(run_myself)
    11968    0.151    0.000    0.223    0.000 map_reduce.py:1292(walk_branch_locally)
...
<pstats.Stats instance at 0x7fedea40c6c8>

Python

>>> from sage.all import *
>>> import cProfile, pstats
>>> st = pstats.Stats(d.name+'0')
>>> st.strip_dirs().sort_stats('cumulative').print_stats()  # random
...
   Ordered by: cumulative time

   ncalls  tottime  percall  cumtime  percall filename:lineno(function)
        1    0.023    0.023    0.432    0.432 map_reduce.py:1211(run_myself)
    11968    0.151    0.000    0.223    0.000 map_reduce.py:1292(walk_branch_locally)
...
<pstats.Stats instance at 0x7fedea40c6c8>

Like a good neighbor we clean up our temporary directory as soon as possible:

Sage

sage: d.cleanup()

Python

>>> from sage.all import *
>>> d.cleanup()

See also

The Python Profilers for more detail on profiling in python.

Logging#

The computation progress is logged through a logging.Logger in sage.parallel.map_reduce.logger together with logging.StreamHandler and a logging.Formatter. They are currently configured to print warning messages to the console.

See also

Logging facility for Python for more detail on logging and log system configuration.

Note

Calls to logger which involve printing the node are commented out in the code, because the printing (to a string) of the node can be very time consuming depending on the node and it happens before the decision whether the logger should record the string or drop it.

How does it work ?#

The scheduling algorithm we use here is any adaptation of Wikipedia article Work_stealing:

In a work stealing scheduler, each processor in a computer system has a queue of work items (computational tasks, threads) to perform. […]. Each work items are initially put on the queue of the processor executing the work item. When a processor runs out of work, it looks at the queues of other processors and “steals” their work items. In effect, work stealing distributes the scheduling work over idle processors, and as long as all processors have work to do, no scheduling overhead occurs.

For communication we use Python’s basic multiprocessing module. We first describe the different actors and communication tools used by the system. The work is done under the coordination of a master object (an instance of RESetMapReduce) by a bunch of worker objects (instances of RESetMapReduceWorker).

Each running map reduce instance works on a RecursivelyEnumeratedSet_forest> called here \(C\) and is coordinated by a RESetMapReduce object called the master. The master is in charge of launching the work, gathering the results and cleaning up at the end of the computation. It doesn’t perform any computation associated to the generation of the element \(C\) nor the computation of the mapped function. It however occasionally perform a reduce, but most reducing is by default done by the workers. Also thanks to the work-stealing algorithm, the master is only involved in detecting the termination of the computation but all the load balancing is done at the level of the workers.

Workers are instances of RESetMapReduceWorker. They are responsible for doing the actual computations: element generation, mapping and reducing. They are also responsible for the load balancing thanks to work-stealing.

Here is a description of the attributes of the master relevant to the map-reduce protocol:

_results – a SimpleQueue where the master gathers the results sent by the workers.
_active_tasks – a Semaphore recording the number of active tasks. The work is complete when it reaches 0.
_done – a Lock which ensures that shutdown is done only once.
_aborted – a Value() storing a shared ctypes.c_bool which is True if the computation was aborted before all workers ran out of work.
_workers – a list of RESetMapReduceWorker objects. Each worker is identified by its position in this list.

Each worker is a process (RESetMapReduceWorker inherits from Process) which contains:

worker._iproc – the identifier of the worker that is its position in the master’s list of workers
worker._todo – a collections.deque storing of nodes of the worker. It is used as a stack by the worker. Thiefs steal from the bottom of this queue.
worker._request – a SimpleQueue storing steal request submitted to worker.
worker._read_task, worker._write_task – a Pipe used to transfer node during steal.
worker._thief – a Thread which is in charge of stealing from worker._todo.

Here is a schematic of the architecture:

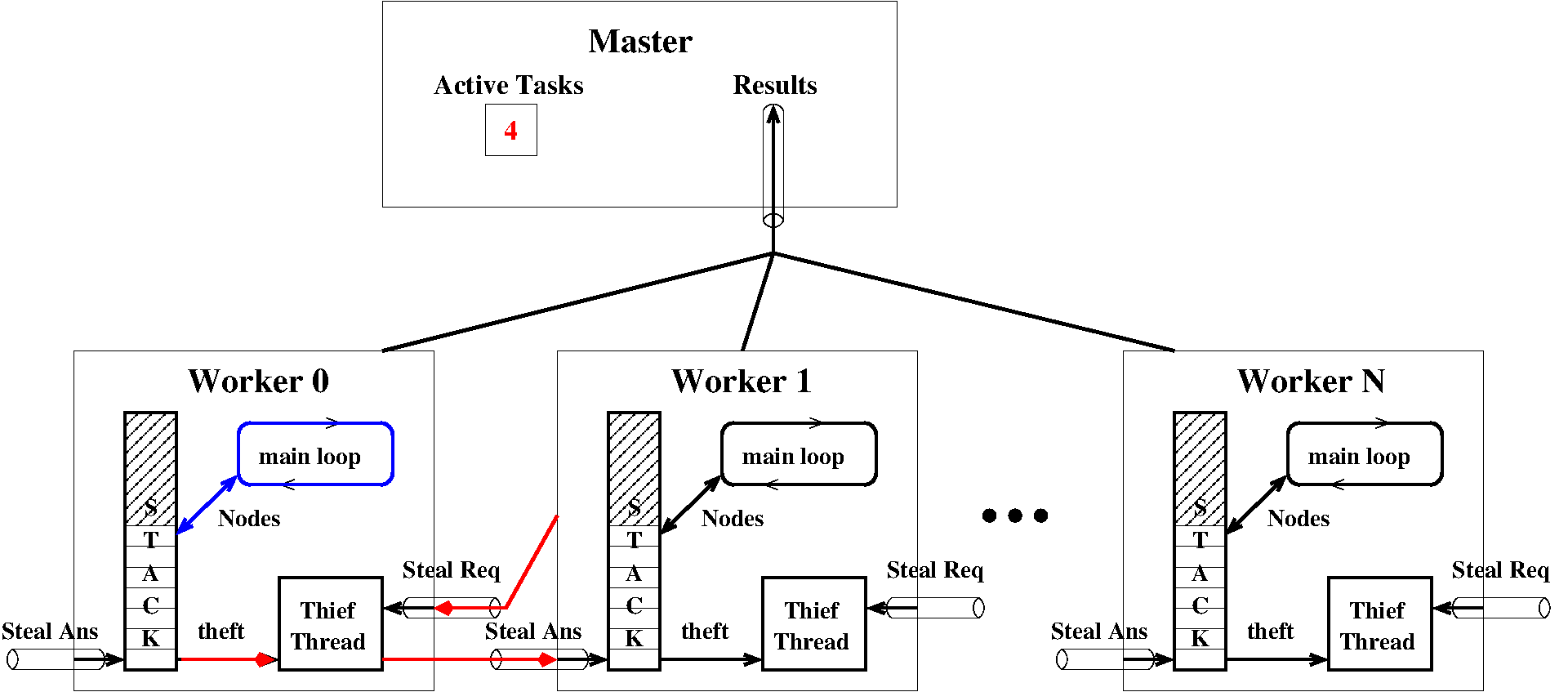
How thefts are performed#

During normal time, that is, when all workers are active, a worker W is iterating though a loop inside RESetMapReduceWorker.walk_branch_locally(). Work nodes are taken from and new nodes W._todo are appended to W._todo. When a worker W runs out of work, that is, when worker._todo is empty, it tries to steal some work (i.e., a node) from another worker. This is performed in the RESetMapReduceWorker.steal() method.

From the point of view of W, here is what happens:

W signals to the master that it is idle: master._signal_task_done;
W chooses a victim V at random;
W sends a request to V: it puts its identifier into V._request;
W tries to read a node from W._read_task. Then three things may happen:
- a proper node is read. Then the theft was a success and W starts working locally on the received node.
- None is received. This means that V was idle. Then W tries another victim.
- AbortError is received. This means either that the computation was aborted or that it simply succeeded and that no more work is required by W. Therefore an AbortError exception is raised leading W to shutdown.

We now describe the protocol on the victim’s side. Each worker process contains a Thread which we call T for thief which acts like some kind of Troyan horse during theft. It is normally blocked waiting for a steal request.

From the point of view of V and T, here is what happens:

during normal time, T is blocked waiting on V._request;
upon steal request, T wakes up receiving the identification of W;
T signals to the master that a new task is starting by master._signal_task_start;
Two things may happen depending if the queue V._todo is empty or not. Remark that due to the GIL, there is no parallel execution between the victim V and its thief thread T.
- If V._todo is empty, then None is answered on W._write_task. The task is immediately signaled to end the master through master._signal_task_done.
- Otherwise, a node is removed from the bottom of V._todo. The node is sent to W on W._write_task. The task will be ended by W, that is, when finished working on the subtree rooted at the node, W will call master._signal_task_done.

The end of the computation#

To detect when a computation is finished, a synchronized integer is kept which counts the number of active tasks. This is essentially a semaphore but semaphores are broken on Darwin OSes so we ship two implementations depending on the OS (see ActiveTaskCounter and ActiveTaskCounterDarwin and the note below).

When a worker finishes working on a task, it calls master._signal_task_done. This decreases the task counter master._active_tasks. When it reaches 0, it means that there are no more nodes: the work is completed. The worker executes master._shutdown which sends AbortError to all worker._request and worker._write_task queues. Each worker or thief thread receiving such a message raises the corresponding exception, therefore stopping its work. A lock called master._done ensures that shutdown is only done once.

Finally, it is also possible to interrupt the computation before its ends, by calling master.abort(). This is achieved by setting master._active_tasks to 0 and calling master._shutdown.

Warning

The macOS Semaphore bug

Darwin OSes do not correctly implement POSIX’s semaphore semantic. Indeed, on these systems, acquire may fail and return False not only when the semaphore is equal to zero but also because someone else is trying to acquire at the same time. This makes using Semaphores impossible on macOS so that on these systems we use a synchronized integer instead.

Are there examples of classes?#

Yes! Here they are:

RESetMPExample – a simple basic example
RESetParallelIterator – a more advanced example using non standard communication configuration.

Tests#

Generating series for the sum of strictly decreasing lists of integers smaller than 15:

Sage

sage: y = polygen(ZZ, 'y')
sage: R = RESetMapReduce(
....:     roots=[([], 0, 0)] + [([i], i, i) for i in range(1, 15)],
....:     children=lambda list_sum_last:
....:         [(list_sum_last[0] + [i], list_sum_last[1] + i, i)
....:          for i in range(1, list_sum_last[2])],
....:     map_function=lambda li_sum_dummy: y**li_sum_dummy[1])
sage: sg = R.run()
sage: sg == prod((1 + y**i) for i in range(1, 15))
True

Python

>>> from sage.all import *
>>> y = polygen(ZZ, 'y')
>>> R = RESetMapReduce(
...     roots=[([], Integer(0), Integer(0))] + [([i], i, i) for i in range(Integer(1), Integer(15))],
...     children=lambda list_sum_last:
...         [(list_sum_last[Integer(0)] + [i], list_sum_last[Integer(1)] + i, i)
...          for i in range(Integer(1), list_sum_last[Integer(2)])],
...     map_function=lambda li_sum_dummy: y**li_sum_dummy[Integer(1)])
>>> sg = R.run()
>>> sg == prod((Integer(1) + y**i) for i in range(Integer(1), Integer(15)))
True

Classes and methods#

exception sage.parallel.map_reduce.AbortError[source]#

Bases: Exception

Exception for aborting parallel computations.

This is used both as exception or as abort message.

sage.parallel.map_reduce.ActiveTaskCounter[source]#: alias of ActiveTaskCounterPosix

class sage.parallel.map_reduce.ActiveTaskCounterDarwin(task_number)[source]#

Bases: object

Handling the number of active tasks.

A class for handling the number of active tasks in a distributed computation process. This is essentially a semaphore, but Darwin OSes do not correctly implement POSIX’s semaphore semantic. So we use a shared integer with a lock.

abort()[source]#

Set the task counter to zero.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import ActiveTaskCounterDarwin as ATC
sage: c = ATC(4); c
ActiveTaskCounter(value=4)
sage: c.abort()
sage: c
ActiveTaskCounter(value=0)

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import ActiveTaskCounterDarwin as ATC
>>> c = ATC(Integer(4)); c
ActiveTaskCounter(value=4)
>>> c.abort()
>>> c
ActiveTaskCounter(value=0)

task_done()[source]#

Decrement the task counter by one.

OUTPUT:

Calling task_done() decrements the counter and returns its new value.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import ActiveTaskCounterDarwin as ATC
sage: c = ATC(4); c
ActiveTaskCounter(value=4)
sage: c.task_done()
3
sage: c
ActiveTaskCounter(value=3)

sage: c = ATC(0)
sage: c.task_done()
-1

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import ActiveTaskCounterDarwin as ATC
>>> c = ATC(Integer(4)); c
ActiveTaskCounter(value=4)
>>> c.task_done()
3
>>> c
ActiveTaskCounter(value=3)

>>> c = ATC(Integer(0))
>>> c.task_done()
-1

task_start()[source]#

Increment the task counter by one.

OUTPUT:

Calling task_start() on a zero or negative counter returns 0, otherwise increment the counter and returns its value after the incrementation.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import ActiveTaskCounterDarwin as ATC
sage: c = ATC(4); c
ActiveTaskCounter(value=4)
sage: c.task_start()
5
sage: c
ActiveTaskCounter(value=5)

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import ActiveTaskCounterDarwin as ATC
>>> c = ATC(Integer(4)); c
ActiveTaskCounter(value=4)
>>> c.task_start()
5
>>> c
ActiveTaskCounter(value=5)

Calling task_start() on a zero counter does nothing:

Sage

sage: c = ATC(0)
sage: c.task_start()
0
sage: c
ActiveTaskCounter(value=0)

Python

>>> from sage.all import *
>>> c = ATC(Integer(0))
>>> c.task_start()
0
>>> c
ActiveTaskCounter(value=0)

class sage.parallel.map_reduce.ActiveTaskCounterPosix(task_number)[source]#

Bases: object

Handling the number of active tasks.

A class for handling the number of active tasks in a distributed computation process. This is the standard implementation on POSIX compliant OSes. We essentially wrap a semaphore.

Note

A legitimate question is whether there is a need in keeping the two implementations. I ran the following experiment on my machine:

S = RecursivelyEnumeratedSet(
        [[]],
        lambda l: ([l[:i] + [len(l)] + l[i:]
                    for i in range(len(l) + 1)]
                   if len(l) < NNN else []),
        structure='forest',
        enumeration='depth')
%time sp = S.map_reduce(lambda z: x**len(z)); sp

For NNN = 10, averaging a dozen of runs, I got:

Posix compliant implementation: 17.04 s
Darwin implementation: 18.26 s

So there is a non negligible overhead. It will probably be worth it if we try to cythonize the code. So I’m keeping both implementations.

abort()[source]#

Set the task counter to zero.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import ActiveTaskCounter as ATC
sage: c = ATC(4); c
ActiveTaskCounter(value=4)
sage: c.abort()
sage: c
ActiveTaskCounter(value=0)

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import ActiveTaskCounter as ATC
>>> c = ATC(Integer(4)); c
ActiveTaskCounter(value=4)
>>> c.abort()
>>> c
ActiveTaskCounter(value=0)

task_done()[source]#

Decrement the task counter by one.

OUTPUT:

Calling task_done() decrements the counter and returns its new value.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import ActiveTaskCounter as ATC
sage: c = ATC(4); c
ActiveTaskCounter(value=4)
sage: c.task_done()
3
sage: c
ActiveTaskCounter(value=3)

sage: c = ATC(0)
sage: c.task_done()
-1

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import ActiveTaskCounter as ATC
>>> c = ATC(Integer(4)); c
ActiveTaskCounter(value=4)
>>> c.task_done()
3
>>> c
ActiveTaskCounter(value=3)

>>> c = ATC(Integer(0))
>>> c.task_done()
-1

task_start()[source]#

Increment the task counter by one.

OUTPUT:

Calling task_start() on a zero or negative counter returns 0, otherwise increment the counter and returns its value after the incrementation.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import ActiveTaskCounterDarwin as ATC
sage: c = ATC(4); c
ActiveTaskCounter(value=4)
sage: c.task_start()
5
sage: c
ActiveTaskCounter(value=5)

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import ActiveTaskCounterDarwin as ATC
>>> c = ATC(Integer(4)); c
ActiveTaskCounter(value=4)
>>> c.task_start()
5
>>> c
ActiveTaskCounter(value=5)

Calling task_start() on a zero counter does nothing:

Sage

sage: c = ATC(0)
sage: c.task_start()
0
sage: c
ActiveTaskCounter(value=0)

Python

>>> from sage.all import *
>>> c = ATC(Integer(0))
>>> c.task_start()
0
>>> c
ActiveTaskCounter(value=0)

class sage.parallel.map_reduce.RESetMPExample(maxl=9)[source]#

Bases: RESetMapReduce

An example of map reduce class.

INPUT:

maxl – the maximum size of permutations generated (default to \(9\)).

This computes the generating series of permutations counted by their size up to size maxl.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample
sage: EX = RESetMPExample()
sage: EX.run()
362880*x^9 + 40320*x^8 + 5040*x^7 + 720*x^6 + 120*x^5
+ 24*x^4 + 6*x^3 + 2*x^2 + x + 1

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample
>>> EX = RESetMPExample()
>>> EX.run()
362880*x^9 + 40320*x^8 + 5040*x^7 + 720*x^6 + 120*x^5
+ 24*x^4 + 6*x^3 + 2*x^2 + x + 1

See also

This is an example of RESetMapReduce

children(l)[source]#

Return the children of the permutation \(l\).

INPUT:

l – a list containing a permutation

OUTPUT:

The lists with len(l) inserted at all possible positions into l.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample
sage: RESetMPExample().children([1,0])
[[2, 1, 0], [1, 2, 0], [1, 0, 2]]

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample
>>> RESetMPExample().children([Integer(1),Integer(0)])
[[2, 1, 0], [1, 2, 0], [1, 0, 2]]

map_function(l)[source]#

The monomial associated to the permutation \(l\).

INPUT:

l – a list containing a permutation

OUTPUT:

The monomial x^len(l).

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample
sage: RESetMPExample().map_function([1,0])
x^2

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample
>>> RESetMPExample().map_function([Integer(1),Integer(0)])
x^2

roots()[source]#

Return the empty permutation.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample
sage: RESetMPExample().roots()
[[]]

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample
>>> RESetMPExample().roots()
[[]]

class sage.parallel.map_reduce.RESetMapReduce(roots=None, children=None, post_process=None, map_function=None, reduce_function=None, reduce_init=None, forest=None)[source]#

Bases: object

Map-Reduce on recursively enumerated sets.

INPUT:

Description of the set:

either forest=f – where f is a RecursivelyEnumeratedSet_forest>
or a triple roots, children, post_process as follows
- roots=r – The root of the enumeration
- children=c – a function iterating through children nodes, given a parent node
- post_process=p – a post-processing function

The option post_process allows for customizing the nodes that are actually produced. Furthermore, if post_process(x) returns None, then x won’t be output at all.

Description of the map/reduce operation:

map_function=f – (default to None)
reduce_function=red – (default to None)
reduce_init=init – (default to None)

See also

the Map/Reduce module for details and examples.

abort()[source]#

Abort the current parallel computation.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetParallelIterator
sage: S = RESetParallelIterator([[]],
....:     lambda l: [l + [0], l + [1]] if len(l) < 17 else [])
sage: it = iter(S)
sage: next(it)  # random
[]
sage: S.abort()
sage: hasattr(S, 'work_queue')
False

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetParallelIterator
>>> S = RESetParallelIterator([[]],
...     lambda l: [l + [Integer(0)], l + [Integer(1)]] if len(l) < Integer(17) else [])
>>> it = iter(S)
>>> next(it)  # random
[]
>>> S.abort()
>>> hasattr(S, 'work_queue')
False

Cleanup:

Sage

sage: S.finish()

Python

>>> from sage.all import *
>>> S.finish()

finish()[source]#

Destroy the workers and all the communication objects.

Communication statistics are gathered before destroying the workers.

See also

print_communication_statistics()

get_results(timeout=None)[source]#

Get the results from the queue.

OUTPUT:

The reduction of the results of all the workers, that is, the result of the map/reduce computation.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMapReduce
sage: S = RESetMapReduce()
sage: S.setup_workers(2)
sage: for v in [1, 2, None, 3, None]: S._results.put(v)
sage: S.get_results()
6

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMapReduce
>>> S = RESetMapReduce()
>>> S.setup_workers(Integer(2))
>>> for v in [Integer(1), Integer(2), None, Integer(3), None]: S._results.put(v)
>>> S.get_results()
6

Cleanup:

Sage

sage: del S._results, S._active_tasks, S._done, S._workers

Python

>>> from sage.all import *
>>> del S._results, S._active_tasks, S._done, S._workers

map_function(o)[source]#

Return the function mapped by self.

INPUT:

o – a node

OUTPUT:

By default 1.

Note

This should be overloaded in applications.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMapReduce
sage: S = RESetMapReduce()
sage: S.map_function(7)
1
sage: S = RESetMapReduce(map_function = lambda x: 3*x + 5)
sage: S.map_function(7)
26

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMapReduce
>>> S = RESetMapReduce()
>>> S.map_function(Integer(7))
1
>>> S = RESetMapReduce(map_function = lambda x: Integer(3)*x + Integer(5))
>>> S.map_function(Integer(7))
26

post_process(a)[source]#

Return the image of a under the post-processing function for self.

INPUT:

a – a node

With the default post-processing function, which is the identity function, this returns a itself.

Note

This should be overloaded in applications.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMapReduce
sage: S = RESetMapReduce()
sage: S.post_process(4)
4
sage: S = RESetMapReduce(post_process=lambda x: x*x)
sage: S.post_process(4)
16

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMapReduce
>>> S = RESetMapReduce()
>>> S.post_process(Integer(4))
4
>>> S = RESetMapReduce(post_process=lambda x: x*x)
>>> S.post_process(Integer(4))
16

print_communication_statistics(blocksize=16)[source]#

Print the communication statistics in a nice way.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample
sage: S = RESetMPExample(maxl=6)
sage: S.run()
720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

sage: S.print_communication_statistics()  # random
#proc:        0    1    2    3    4    5    6    7
reqs sent:    5    2    3   11   21   19    1    0
reqs rcvs:   10   10    9    5    1   11    9    2
- thefs:      1    0    0    0    0    0    0    0
+ thefs:      0    0    1    0    0    0    0    0

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample
>>> S = RESetMPExample(maxl=Integer(6))
>>> S.run()
720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

>>> S.print_communication_statistics()  # random
#proc:        0    1    2    3    4    5    6    7
reqs sent:    5    2    3   11   21   19    1    0
reqs rcvs:   10   10    9    5    1   11    9    2
- thefs:      1    0    0    0    0    0    0    0
+ thefs:      0    0    1    0    0    0    0    0

random_worker()[source]#

Return a random worker.

OUTPUT:

A worker for self chosen at random.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
sage: from threading import Thread
sage: EX = RESetMPExample(maxl=6)
sage: EX.setup_workers(2)
sage: EX.random_worker()
<RESetMapReduceWorker...RESetMapReduceWorker-... initial...>
sage: EX.random_worker() in EX._workers
True

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
>>> from threading import Thread
>>> EX = RESetMPExample(maxl=Integer(6))
>>> EX.setup_workers(Integer(2))
>>> EX.random_worker()
<RESetMapReduceWorker...RESetMapReduceWorker-... initial...>
>>> EX.random_worker() in EX._workers
True

Cleanup:

Sage

sage: del EX._results, EX._active_tasks, EX._done, EX._workers

Python

>>> from sage.all import *
>>> del EX._results, EX._active_tasks, EX._done, EX._workers

reduce_function(a, b)[source]#

Return the reducer function for self.

INPUT:

a, b – two values to be reduced

OUTPUT:

By default the sum of a and b.

Note

This should be overloaded in applications.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMapReduce
sage: S = RESetMapReduce()
sage: S.reduce_function(4, 3)
7
sage: S = RESetMapReduce(reduce_function=lambda x,y: x*y)
sage: S.reduce_function(4, 3)
12

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMapReduce
>>> S = RESetMapReduce()
>>> S.reduce_function(Integer(4), Integer(3))
7
>>> S = RESetMapReduce(reduce_function=lambda x,y: x*y)
>>> S.reduce_function(Integer(4), Integer(3))
12

reduce_init()[source]#: Return the initial element for a reduction.

Note

This should be overloaded in applications.

roots()[source]#

Return the roots of self.

OUTPUT:

An iterable of nodes.

Note

This should be overloaded in applications.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMapReduce
sage: S = RESetMapReduce(42)
sage: S.roots()
42

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMapReduce
>>> S = RESetMapReduce(Integer(42))
>>> S.roots()
42

run(max_proc=None, reduce_locally=True, timeout=None, profile=None)[source]#

Run the computations.

INPUT:

max_proc – (integer, default: None) if given, the maximum number of worker processors to use. The actual number is also bounded by the value of the environment variable SAGE_NUM_THREADS (the number of cores by default).
reduce_locally – See RESetMapReduceWorker (default: True)
timeout – a timeout on the computation (default: None)
profile – directory/filename prefix for profiling, or None for no profiling (default: None)

OUTPUT:

The result of the map/reduce computation or an exception AbortError if the computation was interrupted or timeout.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample
sage: EX = RESetMPExample(maxl = 8)
sage: EX.run()
40320*x^8 + 5040*x^7 + 720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample
>>> EX = RESetMPExample(maxl = Integer(8))
>>> EX.run()
40320*x^8 + 5040*x^7 + 720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

Here is an example or how to deal with timeout:

Sage

sage: from sage.parallel.map_reduce import AbortError
sage: EX = RESetMPExample(maxl = 100)
sage: try:
....:     res = EX.run(timeout=float(0.01))
....: except AbortError:
....:     print("Computation timeout")
....: else:
....:     print("Computation normally finished")
....:     res
Computation timeout

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import AbortError
>>> EX = RESetMPExample(maxl = Integer(100))
>>> try:
...     res = EX.run(timeout=float(RealNumber('0.01')))
... except AbortError:
...     print("Computation timeout")
... else:
...     print("Computation normally finished")
...     res
Computation timeout

The following should not timeout even on a very slow machine:

Sage

sage: from sage.parallel.map_reduce import AbortError
sage: EX = RESetMPExample(maxl = 8)
sage: try:
....:     res = EX.run(timeout=60)
....: except AbortError:
....:     print("Computation Timeout")
....: else:
....:     print("Computation normally finished")
....:     res
Computation normally finished
40320*x^8 + 5040*x^7 + 720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import AbortError
>>> EX = RESetMPExample(maxl = Integer(8))
>>> try:
...     res = EX.run(timeout=Integer(60))
... except AbortError:
...     print("Computation Timeout")
... else:
...     print("Computation normally finished")
...     res
Computation normally finished
40320*x^8 + 5040*x^7 + 720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

run_serial()[source]#

Run the computation serially (mostly for tests).

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample
sage: EX = RESetMPExample(maxl = 4)
sage: EX.run_serial()
24*x^4 + 6*x^3 + 2*x^2 + x + 1

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample
>>> EX = RESetMPExample(maxl = Integer(4))
>>> EX.run_serial()
24*x^4 + 6*x^3 + 2*x^2 + x + 1

setup_workers(max_proc=None, reduce_locally=True)[source]#

Setup the communication channels.

INPUT:

max_proc – (integer) an upper bound on the number of worker processes.
reduce_locally – whether the workers should reduce locally their work or sends results to the master as soon as possible. See RESetMapReduceWorker for details.

start_workers()[source]#

Launch the workers.

The workers should have been created using setup_workers().

class sage.parallel.map_reduce.RESetMapReduceWorker(mapred, iproc, reduce_locally)[source]#

Bases: ForkProcess

Worker for generate-map-reduce.

This shouldn’t be called directly, but instead created by RESetMapReduce.setup_workers().

INPUT:

mapred – the instance of RESetMapReduce for which this process is working.
iproc – the id of this worker.
reduce_locally – when reducing the results. Three possible values are supported:
- True – means the reducing work is done all locally, the result is only sent back at the end of the work. This ensure the lowest level of communication.
- False – results are sent back after each finished branches, when the process is asking for more work.

run()[source]#

The main function executed by the worker.

Calls run_myself() after possibly setting up parallel profiling.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
sage: EX = RESetMPExample(maxl=6)
sage: EX.setup_workers(1)

sage: w = EX._workers[0]
sage: w._todo.append(EX.roots()[0])

sage: w.run()
sage: sleep(int(1))
sage: w._todo.append(None)

sage: EX.get_results()
720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
>>> EX = RESetMPExample(maxl=Integer(6))
>>> EX.setup_workers(Integer(1))

>>> w = EX._workers[Integer(0)]
>>> w._todo.append(EX.roots()[Integer(0)])

>>> w.run()
>>> sleep(int(Integer(1)))
>>> w._todo.append(None)

>>> EX.get_results()
720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

Cleanups:

Sage

sage: del EX._results, EX._active_tasks, EX._done, EX._workers

Python

>>> from sage.all import *
>>> del EX._results, EX._active_tasks, EX._done, EX._workers

run_myself()[source]#

The main function executed by the worker.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
sage: EX = RESetMPExample(maxl=6)
sage: EX.setup_workers(1)

sage: w = EX._workers[0]
sage: w._todo.append(EX.roots()[0])
sage: w.run_myself()

sage: sleep(int(1))
sage: w._todo.append(None)

sage: EX.get_results()
720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
>>> EX = RESetMPExample(maxl=Integer(6))
>>> EX.setup_workers(Integer(1))

>>> w = EX._workers[Integer(0)]
>>> w._todo.append(EX.roots()[Integer(0)])
>>> w.run_myself()

>>> sleep(int(Integer(1)))
>>> w._todo.append(None)

>>> EX.get_results()
720*x^6 + 120*x^5 + 24*x^4 + 6*x^3 + 2*x^2 + x + 1

Cleanups:

Sage

sage: del EX._results, EX._active_tasks, EX._done, EX._workers

Python

>>> from sage.all import *
>>> del EX._results, EX._active_tasks, EX._done, EX._workers

send_partial_result()[source]#

Send results to the MapReduce process.

Send the result stored in self._res to the master and reinitialize it to master.reduce_init.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
sage: EX = RESetMPExample(maxl=4)
sage: EX.setup_workers(1)
sage: w = EX._workers[0]
sage: w._res = 4
sage: w.send_partial_result()
sage: w._res
0
sage: EX._results.get()
4

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
>>> EX = RESetMPExample(maxl=Integer(4))
>>> EX.setup_workers(Integer(1))
>>> w = EX._workers[Integer(0)]
>>> w._res = Integer(4)
>>> w.send_partial_result()
>>> w._res
0
>>> EX._results.get()
4

steal()[source]#

Steal some node from another worker.

OUTPUT:

A node stolen from another worker chosen at random.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
sage: from threading import Thread
sage: EX = RESetMPExample(maxl=6)
sage: EX.setup_workers(2)

sage: # known bug (Issue #27537)
sage: w0, w1 = EX._workers
sage: w0._todo.append(42)
sage: thief0 = Thread(target = w0._thief, name="Thief")
sage: thief0.start()
sage: w1.steal()
42
sage: w0._todo
deque([])

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
>>> from threading import Thread
>>> EX = RESetMPExample(maxl=Integer(6))
>>> EX.setup_workers(Integer(2))

>>> # known bug (Issue #27537)
>>> w0, w1 = EX._workers
>>> w0._todo.append(Integer(42))
>>> thief0 = Thread(target = w0._thief, name="Thief")
>>> thief0.start()
>>> w1.steal()
42
>>> w0._todo
deque([])

walk_branch_locally(node)[source]#

Work locally.

Performs the map/reduce computation on the subtrees rooted at node.

INPUT:

node – the root of the subtree explored.

OUTPUT:

Nothing, the result are stored in self._res.

This is where the actual work is performed.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
sage: EX = RESetMPExample(maxl=4)
sage: w = RESetMapReduceWorker(EX, 0, True)
sage: def sync(): pass
sage: w.synchronize = sync
sage: w._res = 0

sage: w.walk_branch_locally([])
sage: w._res
x^4 + x^3 + x^2 + x + 1

sage: w.walk_branch_locally(w._todo.pop())
sage: w._res
2*x^4 + x^3 + x^2 + x + 1

sage: while True: w.walk_branch_locally(w._todo.pop())
Traceback (most recent call last):
...
IndexError: pop from an empty deque
sage: w._res
24*x^4 + 6*x^3 + 2*x^2 + x + 1

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetMPExample, RESetMapReduceWorker
>>> EX = RESetMPExample(maxl=Integer(4))
>>> w = RESetMapReduceWorker(EX, Integer(0), True)
>>> def sync(): pass
>>> w.synchronize = sync
>>> w._res = Integer(0)

>>> w.walk_branch_locally([])
>>> w._res
x^4 + x^3 + x^2 + x + 1

>>> w.walk_branch_locally(w._todo.pop())
>>> w._res
2*x^4 + x^3 + x^2 + x + 1

>>> while True: w.walk_branch_locally(w._todo.pop())
Traceback (most recent call last):
...
IndexError: pop from an empty deque
>>> w._res
24*x^4 + 6*x^3 + 2*x^2 + x + 1

class sage.parallel.map_reduce.RESetParallelIterator(roots=None, children=None, post_process=None, map_function=None, reduce_function=None, reduce_init=None, forest=None)[source]#

Bases: RESetMapReduce

A parallel iterator for recursively enumerated sets.

This demonstrates how to use RESetMapReduce to get an iterator on a recursively enumerated set for which the computations are done in parallel.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetParallelIterator
sage: S = RESetParallelIterator([[]],
....:     lambda l: [l + [0], l + [1]] if len(l) < 15 else [])
sage: sum(1 for _ in S)
65535

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetParallelIterator
>>> S = RESetParallelIterator([[]],
...     lambda l: [l + [Integer(0)], l + [Integer(1)]] if len(l) < Integer(15) else [])
>>> sum(Integer(1) for _ in S)
65535

map_function(z)[source]#

Return a singleton tuple.

INPUT:

z – a node

OUTPUT:

The singleton (z, ).

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import RESetParallelIterator
sage: S = RESetParallelIterator( [[]],
....:     lambda l: [l + [0], l + [1]] if len(l) < 15 else [])
sage: S.map_function([1, 0])
([1, 0],)

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import RESetParallelIterator
>>> S = RESetParallelIterator( [[]],
...     lambda l: [l + [Integer(0)], l + [Integer(1)]] if len(l) < Integer(15) else [])
>>> S.map_function([Integer(1), Integer(0)])
([1, 0],)

reduce_init#: alias of tuple

sage.parallel.map_reduce.proc_number(max_proc=None)[source]#

Return the number of processes to use.

INPUT:

max_proc – an upper bound on the number of processes or None.

EXAMPLES:

Sage

sage: from sage.parallel.map_reduce import proc_number
sage: proc_number()  # random
8
sage: proc_number(max_proc=1)
1
sage: proc_number(max_proc=2) in (1, 2)
True

Python

>>> from sage.all import *
>>> from sage.parallel.map_reduce import proc_number
>>> proc_number()  # random
8
>>> proc_number(max_proc=Integer(1))
1
>>> proc_number(max_proc=Integer(2)) in (Integer(1), Integer(2))
True

Parallel computations using RecursivelyEnumeratedSet and Map-Reduce#

Contents#

How is this different from usual MapReduce?#

How can I use all that stuff?#

Advanced use#

Profiling#

Logging#

How does it work ?#

How thefts are performed#

The end of the computation#

Are there examples of classes?#

Tests#

Classes and methods#