A Sage bemutatása¶
Ez a Sage-nek egy olyan bemutatása, amely pontosan követi a Mathematica bemutatását, ami a „Mathematica Book” könyv elején található.
A Sage, mint számológép¶
A Sage parancssora tartalmaz egy sage: promptot; ezt nem kell
beírnod. Ha a Sage jegyzetfüzetet (Sage notebook) használod, akkor
írj be mindent, ami a sage: prompt után van, egy beviteli mezőbe,
majd nyomj shift-enter-t a hozzá tartozó kimenet kiszámításához.
sage: 3 + 5
8
>>> from sage.all import *
>>> Integer(3) + Integer(5)
8
A kalap jel a hatványra emelést jelenti.
sage: 57.1 ^ 100
4.60904368661396e175
>>> from sage.all import *
>>> RealNumber('57.1') ** Integer(100)
4.60904368661396e175
Kiszámítjuk egy \(2 \times 2\)-es mátrix inverzét Sage-ben.
sage: matrix([[1,2], [3,4]])^(-1)
[ -2 1]
[ 3/2 -1/2]
>>> from sage.all import *
>>> matrix([[Integer(1),Integer(2)], [Integer(3),Integer(4)]])**(-Integer(1))
[ -2 1]
[ 3/2 -1/2]
Itt egy egyszerű függvényt integrálunk.
sage: x = var('x') # szimbolikus változót hozunk létre
sage: integrate(sqrt(x)*sqrt(1+x), x)
1/4*((x + 1)^(3/2)/x^(3/2) + sqrt(x + 1)/sqrt(x))/((x + 1)^2/x^2 - 2*(x + 1)/x + 1) - 1/8*log(sqrt(x + 1)/sqrt(x) + 1) + 1/8*log(sqrt(x + 1)/sqrt(x) - 1)
>>> from sage.all import *
>>> x = var('x') # szimbolikus változót hozunk létre
>>> integrate(sqrt(x)*sqrt(Integer(1)+x), x)
1/4*((x + 1)^(3/2)/x^(3/2) + sqrt(x + 1)/sqrt(x))/((x + 1)^2/x^2 - 2*(x + 1)/x + 1) - 1/8*log(sqrt(x + 1)/sqrt(x) + 1) + 1/8*log(sqrt(x + 1)/sqrt(x) - 1)
Ez azt kéri a Sage-től, hogy egy másodfokú egyenletet oldjon meg.
A == jel felel meg az egyenlőségnek a Sage-ben.
sage: a = var('a')
sage: S = solve(x^2 + x == a, x); S
[x == -1/2*sqrt(4*a + 1) - 1/2, x == 1/2*sqrt(4*a + 1) - 1/2]
>>> from sage.all import *
>>> a = var('a')
>>> S = solve(x**Integer(2) + x == a, x); S
[x == -1/2*sqrt(4*a + 1) - 1/2, x == 1/2*sqrt(4*a + 1) - 1/2]
Az eredmény egyenleteknek a listája.
sage: S[0].rhs()
-1/2*sqrt(4*a + 1) - 1/2
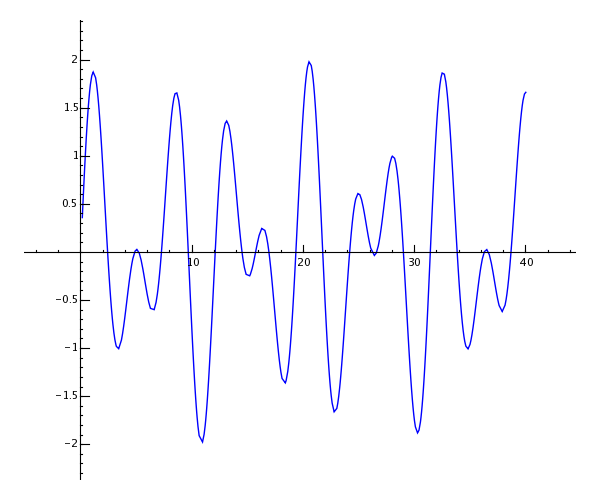
sage: show(plot(sin(x) + sin(1.6*x), 0, 40))
>>> from sage.all import *
>>> S[Integer(0)].rhs()
-1/2*sqrt(4*a + 1) - 1/2
>>> show(plot(sin(x) + sin(RealNumber('1.6')*x), Integer(0), Integer(40)))
Nagyteljesítményű számítások Sage-dzsel¶
Először létrehozzuk véletlen számoknak egy \(500 \times 500\) mátrixát.
sage: m = random_matrix(RDF,500)
>>> from sage.all import *
>>> m = random_matrix(RDF,Integer(500))
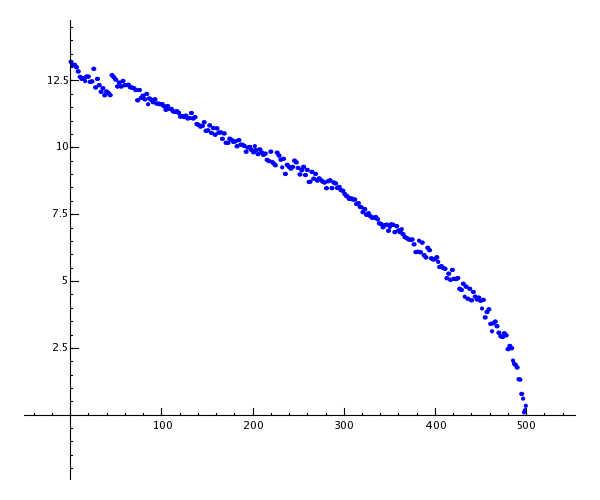
A Sage-nek néhány másodpercet vesz igénybe, hogy kiszámítsa a mátrix sajátértékeit, és ábrázolja őket.
sage: e = m.eigenvalues() #körülbelül 2 másodperc
sage: w = [(i, abs(e[i])) for i in range(len(e))]
sage: show(points(w))
>>> from sage.all import *
>>> e = m.eigenvalues() #körülbelül 2 másodperc
>>> w = [(i, abs(e[i])) for i in range(len(e))]
>>> show(points(w))
A GNU sokféle pontosságú könyvtárnak (GNU Multiprecision Library (GMP)) köszönhetően a Sage nagyon nagy számokat tud kezelni, még millió vagy milliárd számjegyből álló számokat is.
sage: factorial(100)
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
sage: n = factorial(1000000) #körülbelül 2.5 másodperc
>>> from sage.all import *
>>> factorial(Integer(100))
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
>>> n = factorial(Integer(1000000)) #körülbelül 2.5 másodperc
Ez a \(\pi\)-nek legalább 100 számjegyét számítja ki.
sage: N(pi, digits=100)
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068
>>> from sage.all import *
>>> N(pi, digits=Integer(100))
3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117068
Ez azt kéri a Sage-től, hogy egy két változós polinomot szorzattá alakítson.
sage: R.<x,y> = QQ[]
sage: F = factor(x^99 + y^99)
sage: F
(x + y) * (x^2 - x*y + y^2) * (x^6 - x^3*y^3 + y^6) *
(x^10 - x^9*y + x^8*y^2 - x^7*y^3 + x^6*y^4 - x^5*y^5 +
x^4*y^6 - x^3*y^7 + x^2*y^8 - x*y^9 + y^10) *
(x^20 + x^19*y - x^17*y^3 - x^16*y^4 + x^14*y^6 + x^13*y^7 -
x^11*y^9 - x^10*y^10 - x^9*y^11 + x^7*y^13 + x^6*y^14 -
x^4*y^16 - x^3*y^17 + x*y^19 + y^20) * (x^60 + x^57*y^3 -
x^51*y^9 - x^48*y^12 + x^42*y^18 + x^39*y^21 - x^33*y^27 -
x^30*y^30 - x^27*y^33 + x^21*y^39 + x^18*y^42 - x^12*y^48 -
x^9*y^51 + x^3*y^57 + y^60)
sage: F.expand()
x^99 + y^99
>>> from sage.all import *
>>> R = QQ['x, y']; (x, y,) = R._first_ngens(2)
>>> F = factor(x**Integer(99) + y**Integer(99))
>>> F
(x + y) * (x^2 - x*y + y^2) * (x^6 - x^3*y^3 + y^6) *
(x^10 - x^9*y + x^8*y^2 - x^7*y^3 + x^6*y^4 - x^5*y^5 +
x^4*y^6 - x^3*y^7 + x^2*y^8 - x*y^9 + y^10) *
(x^20 + x^19*y - x^17*y^3 - x^16*y^4 + x^14*y^6 + x^13*y^7 -
x^11*y^9 - x^10*y^10 - x^9*y^11 + x^7*y^13 + x^6*y^14 -
x^4*y^16 - x^3*y^17 + x*y^19 + y^20) * (x^60 + x^57*y^3 -
x^51*y^9 - x^48*y^12 + x^42*y^18 + x^39*y^21 - x^33*y^27 -
x^30*y^30 - x^27*y^33 + x^21*y^39 + x^18*y^42 - x^12*y^48 -
x^9*y^51 + x^3*y^57 + y^60)
>>> F.expand()
x^99 + y^99
A Sage-nek kevesebb mint 5 másodpercbe telik, hogy kiszámítsa, hogy a százmilliót hányféle képpen lehet pozitív egész számok összegeként felírni.
sage: z = Partitions(10^8).cardinality() #körülbelül 4.5 másodperc
sage: str(z)[:40]
'1760517045946249141360373894679135204009'
>>> from sage.all import *
>>> z = Partitions(Integer(10)**Integer(8)).cardinality() #körülbelül 4.5 másodperc
>>> str(z)[:Integer(40)]
'1760517045946249141360373894679135204009'
Algoritmusokhoz való hozzáférés Sage-ben¶
Amikor a Sage-et használod, akkor a világ egyik legnagyobb szabad forráskódú számítási algoritmus gyűjteményhez férsz hozzá.