Introduction to combinatorics in Sage¶
This thematic tutorial is a translation by Hugh Thomas of the
combinatorics chapter written by Nicolas M. Thiéry in the book “Calcul
Mathématique avec Sage” [CMS2012]. It covers mainly the treatment in
Sage of the following combinatorial problems: enumeration (how
many elements are there in a set \(S\)?), listing (generate all the
elements of \(S\), or iterate through them), and random selection
(choosing an element at random from a set \(S\) according to a given
distribution, for example the uniform distribution). These questions
arise naturally in the calculation of probabilities (what is the
probability in poker of obtaining a straight or a four-of-a-kind of
aces?), in statistical physics, and also in computer algebra (the number
of elements in a finite field), or in the analysis of
algorithms. Combinatorics covers a much wider domain (partial orders,
representation theory, …) for which we only give a few pointers
towards the possibilities offered by Sage.
Todo
Add link to some thematic tutorial on graphs
A characteristic of computational combinatorics is the profusion of types of objects and sets that one wants to manipulate. It would be impossible to describe them all or, a fortiori, to implement them all. After some Initial examples, this chapter illustrates the underlying method: supplying the basic building blocks to describe common combinatorial sets Common enumerated sets, tools for combining them to construct new examples Constructions, and generic algorithms for solving uniformly a large class of problems Generic algorithms.
This is a domain in which Sage has much more extensive capabilities
than most computer algebra systems, and it is rapidly expanding; at the
same time, it is still quite new, and has many unnecessary limitations
and incoherences.
Initial examples¶
Poker and probability¶
We begin by solving a classic problem: enumerating certain combinations of cards in the game of poker, in order to deduce their probability.
A card in a poker deck is characterized by a suit (hearts, diamonds, spades, or clubs) and a value (2, 3, …, 10, jack, queen, king, ace). The game is played with a full deck, which consists of the Cartesian product of the set of suits and the set of values:
We construct these examples in Sage:
sage: Suits = Set(["Hearts", "Diamonds", "Spades", "Clubs"])
sage: Values = Set([2, 3, 4, 5, 6, 7, 8, 9, 10,
....: "Jack", "Queen", "King", "Ace"])
sage: Cards = cartesian_product([Values, Suits])
>>> from sage.all import *
>>> Suits = Set(["Hearts", "Diamonds", "Spades", "Clubs"])
>>> Values = Set([Integer(2), Integer(3), Integer(4), Integer(5), Integer(6), Integer(7), Integer(8), Integer(9), Integer(10),
... "Jack", "Queen", "King", "Ace"])
>>> Cards = cartesian_product([Values, Suits])
There are \(4\) suits and \(13\) possible values, and therefore \(4\times 13=52\) cards in the poker deck:
sage: Suits.cardinality()
4
sage: Values.cardinality()
13
sage: Cards.cardinality()
52
>>> from sage.all import *
>>> Suits.cardinality()
4
>>> Values.cardinality()
13
>>> Cards.cardinality()
52
Draw a card at random:
sage: Cards.random_element() # random
(6, 'Clubs')
>>> from sage.all import *
>>> Cards.random_element() # random
(6, 'Clubs')
Now we can define a set of cards:
sage: Set([Cards.random_element(), Cards.random_element()]) # random
{(2, 'Hearts'), (4, 'Spades')}
>>> from sage.all import *
>>> Set([Cards.random_element(), Cards.random_element()]) # random
{(2, 'Hearts'), (4, 'Spades')}
This problem should eventually disappear: it is planned to change the implementation of Cartesian products so that their elements are immutable by default.
Returning to our main topic, we will be considering a simplified version of poker, in which each player directly draws five cards, which form his hand. The cards are all distinct and the order in which they are drawn is irrelevant; a hand is therefore a subset of size \(5\) of the set of cards. To draw a hand at random, we first construct the set of all possible hands, and then we ask for a randomly chosen element:
sage: Hands = Subsets(Cards, 5)
sage: Hands.random_element() # random
{(4, 'Hearts', 4), (9, 'Diamonds'), (8, 'Spades'),
(9, 'Clubs'), (7, 'Hearts')}
>>> from sage.all import *
>>> Hands = Subsets(Cards, Integer(5))
>>> Hands.random_element() # random
{(4, 'Hearts', 4), (9, 'Diamonds'), (8, 'Spades'),
(9, 'Clubs'), (7, 'Hearts')}
The total number of hands is given by the number of subsets of size \(5\) of a set of size \(52\), which is given by the binomial coefficient \(\binom{52}{5}\):
sage: binomial(52,5)
2598960
>>> from sage.all import *
>>> binomial(Integer(52),Integer(5))
2598960
One can also ignore the method of calculation, and simply ask for the size of the set of hands:
sage: Hands.cardinality()
2598960
>>> from sage.all import *
>>> Hands.cardinality()
2598960
The strength of a poker hand depends on the particular combination of cards present. One such combination is the flush; this is a hand all of whose cards have the same suit. (In principle, straight flushes should be excluded; this will be the goal of an exercise given below.) Such a hand is therefore characterized by the choice of five values from among the thirteen possibilities, and the choice of one of four suits. We will construct the set of all flushes, so as to determine how many there are:
sage: Flushes = cartesian_product([Subsets(Values, 5), Suits])
sage: Flushes.cardinality()
5148
>>> from sage.all import *
>>> Flushes = cartesian_product([Subsets(Values, Integer(5)), Suits])
>>> Flushes.cardinality()
5148
The probability of obtaining a flush when drawing a hand at random is therefore:
sage: Flushes.cardinality() / Hands.cardinality()
33/16660
>>> from sage.all import *
>>> Flushes.cardinality() / Hands.cardinality()
33/16660
or about two in a thousand:
sage: 1000.0 * Flushes.cardinality() / Hands.cardinality()
1.98079231692677
>>> from sage.all import *
>>> RealNumber('1000.0') * Flushes.cardinality() / Hands.cardinality()
1.98079231692677
We will now attempt a little numerical simulation. The following function tests whether a given hand is a flush or not:
sage: def is_flush(hand):
....: return len(set(suit for (val, suit) in hand)) == 1
>>> from sage.all import *
>>> def is_flush(hand):
... return len(set(suit for (val, suit) in hand)) == Integer(1)
We now draw 10000 hands at random, and count the number of flushes obtained (this takes about 10 seconds):
sage: n = 10000
sage: nflush = 0
sage: for i in range(n): # long time
....: hand = Hands.random_element()
....: if is_flush(hand):
....: nflush += 1
sage: n, nflush # random
(10000, 18)
>>> from sage.all import *
>>> n = Integer(10000)
>>> nflush = Integer(0)
>>> for i in range(n): # long time
... hand = Hands.random_element()
... if is_flush(hand):
... nflush += Integer(1)
>>> n, nflush # random
(10000, 18)
Enumeration of trees using generating functions¶
In this section, we discuss the example of complete binary trees, and illustrate in this context many techniques of enumeration in which formal power series play a natural role. These techniques are quite general, and can be applied whenever the combinatorial objects in question admit a recursive definition (grammar) (see Species, decomposable combinatorial classes for an automated treatment). The goal is not a formal presentation of these methods; the calculations are rigorous, but most of the justifications will be skipped.
A complete binary tree is either a leaf \(\mathrm{L}\), or a node to which two complete binary trees are attached (see Figure: The five complete binary trees with four leaves).

Figure: The five complete binary trees with four leaves¶
Our goal is to determine the number \(c_n\) of complete binary trees with \(n\) leaves (in this section, except when explicitly stated otherwise, “trees” always means complete binary trees). This is a typical situation in which one is not only interested in a single set, but in a family of sets, typically parameterized by \(n\in \NN\).
According to the solution of Exercise: enumeration of binary trees, the first terms are given by \(c_1,\dots,c_5=1,1,2,5,14\). The simple fact of knowing these few numbers is already very valuable. In fact, this permits research in a gold mine of information: the Online Encyclopedia of Integer Sequences, commonly called “Sloane”, the name of its principal author, which contains more than 190000 sequences of integers:
sage: oeis([1,1,2,5,14]) # optional -- internet
0: A000108: Catalan numbers: ...
1: ...
2: ...
>>> from sage.all import *
>>> oeis([Integer(1),Integer(1),Integer(2),Integer(5),Integer(14)]) # optional -- internet
0: A000108: Catalan numbers: ...
1: ...
2: ...
The result suggests that the trees are counted by one of the most famous sequences, the Catalan numbers. Looking through the references supplied by the Encyclopedia, we see that this is really the case: the few numbers above form a digital fingerprint of our objects, which enable us to find, in a few seconds, a precise result from within an abundant literature.
Our next goal is to recover this result using Sage. Let
\(C_n\) be the set of trees with \(n\) leaves, so that
\(c_n=|C_n|\); by convention, we will define
\(C_0=\emptyset\) and \(c_0=0\). The set of all trees is
then the disjoint union of the sets \(C_n\):
Having named the set \(C\) of all trees, we can translate the recursive definition of trees into a set-theoretic equation:
In words: a tree \(t\) (which is by definition in \(C\)) is either a leaf (so in \(\{\mathrm{L}\}\)) or a node to which two trees \(t_1\) and \(t_2\) have been attached, and which we can therefore identify with the pair \((t_1,t_2)\) (in the Cartesian product \(C\times C\)).
The founding idea of algebraic combinatorics, introduced by Euler in a letter to Goldbach of 1751 to treat a similar problem , is to manipulate all the numbers \(c_n\) simultaneously, by encoding them as coefficients in a formal power series, called the generating function of the \(c_n\)’s:
where \(z\) is a formal variable (which means that we do not have to worry about questions of convergence). The beauty of this idea is that set-theoretic operations \((A\uplus B\), \(A\times B)\) translate naturally into algebraic operations on the corresponding series (\(A(z)+B(z)\), \(A(z)\cdot B(z)\)), in such a way that the set-theoretic equation satisfied by \(C\) can be translated directly into an algebraic equation satisfied by \(C(z)\):
Now we can solve this equation with Sage. In order to do so, we
introduce two variables, \(C\) and \(z\), and we define the
equation:
sage: C, z = var('C,z') # needs sage.symbolic
sage: sys = [ C == z + C*C ] # needs sage.symbolic
>>> from sage.all import *
>>> C, z = var('C,z') # needs sage.symbolic
>>> sys = [ C == z + C*C ] # needs sage.symbolic
There are two solutions, which happen to have closed forms:
sage: sol = solve(sys, C, solution_dict=True); sol # needs sage.symbolic
[{C: -1/2*sqrt(-4*z + 1) + 1/2}, {C: 1/2*sqrt(-4*z + 1) + 1/2}]
sage: s0 = sol[0][C]; s1 = sol[1][C] # needs sage.symbolic
>>> from sage.all import *
>>> sol = solve(sys, C, solution_dict=True); sol # needs sage.symbolic
[{C: -1/2*sqrt(-4*z + 1) + 1/2}, {C: 1/2*sqrt(-4*z + 1) + 1/2}]
>>> s0 = sol[Integer(0)][C]; s1 = sol[Integer(1)][C] # needs sage.symbolic
and whose Taylor series begin as follows:
sage: s0.series(z, 6) # needs sage.symbolic
1*z + 1*z^2 + 2*z^3 + 5*z^4 + 14*z^5 + Order(z^6)
sage: s1.series(z, 6) # needs sage.symbolic
1 + (-1)*z + (-1)*z^2 + (-2)*z^3 + (-5)*z^4 + (-14)*z^5
+ Order(z^6)
>>> from sage.all import *
>>> s0.series(z, Integer(6)) # needs sage.symbolic
1*z + 1*z^2 + 2*z^3 + 5*z^4 + 14*z^5 + Order(z^6)
>>> s1.series(z, Integer(6)) # needs sage.symbolic
1 + (-1)*z + (-1)*z^2 + (-2)*z^3 + (-5)*z^4 + (-14)*z^5
+ Order(z^6)
The second solution is clearly aberrant, while the first one gives the expected coefficients. Therefore, we set:
sage: C = s0 # needs sage.symbolic
>>> from sage.all import *
>>> C = s0 # needs sage.symbolic
We can now calculate the next terms:
sage: C.series(z, 11) # needs sage.symbolic
1*z + 1*z^2 + 2*z^3 + 5*z^4 + 14*z^5 + 42*z^6 +
132*z^7 + 429*z^8 + 1430*z^9 + 4862*z^10 + Order(z^11)
>>> from sage.all import *
>>> C.series(z, Integer(11)) # needs sage.symbolic
1*z + 1*z^2 + 2*z^3 + 5*z^4 + 14*z^5 + 42*z^6 +
132*z^7 + 429*z^8 + 1430*z^9 + 4862*z^10 + Order(z^11)
or calculate, more or less instantaneously, the 100-th coefficient:
sage: C.series(z, 101).coefficient(z,100) # needs sage.symbolic
227508830794229349661819540395688853956041682601541047340
>>> from sage.all import *
>>> C.series(z, Integer(101)).coefficient(z,Integer(100)) # needs sage.symbolic
227508830794229349661819540395688853956041682601541047340
It is unfortunate to have to recalculate everything if at some point we
wanted the 101-st coefficient. Lazy power series (see
sage.rings.lazy_series_ring) come into their own here, in that
one can define them from a system of equations without solving it, and,
in particular, without needing a closed form for the answer. We begin by
defining the ring of lazy power series:
sage: L.<z> = LazyPowerSeriesRing(QQ)
>>> from sage.all import *
>>> L = LazyPowerSeriesRing(QQ, names=('z',)); (z,) = L._first_ngens(1)
Then we create a “free” power series, which we name, and which we then define by a recursive equation:
sage: C = L.undefined(valuation=1)
sage: C.define(z + C * C)
>>> from sage.all import *
>>> C = L.undefined(valuation=Integer(1))
>>> C.define(z + C * C)
sage: [C.coefficient(i) for i in range(11)]
[0, 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862]
>>> from sage.all import *
>>> [C.coefficient(i) for i in range(Integer(11))]
[0, 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862]
At any point, one can ask for any coefficient without having to redefine \(C\):
sage: C.coefficient(100)
227508830794229349661819540395688853956041682601541047340
sage: C.coefficient(200)
129013158064429114001222907669676675134349530552728882499810851598901419013348319045534580850847735528275750122188940
>>> from sage.all import *
>>> C.coefficient(Integer(100))
227508830794229349661819540395688853956041682601541047340
>>> C.coefficient(Integer(200))
129013158064429114001222907669676675134349530552728882499810851598901419013348319045534580850847735528275750122188940
We now return to the closed form of \(C(z)\):
sage: z = var('z') # needs sage.symbolic
sage: C = s0; C # needs sage.symbolic
-1/2*sqrt(-4*z + 1) + 1/2
>>> from sage.all import *
>>> z = var('z') # needs sage.symbolic
>>> C = s0; C # needs sage.symbolic
-1/2*sqrt(-4*z + 1) + 1/2
The \(n\)-th coefficient in the Taylor series for \(C(z)\) being given by \(\frac{1}{n!} C(z)^{(n)}(0)\), we look at the successive derivatives \(C(z)^{(n)}(z)\):
sage: derivative(C, z, 1) # needs sage.symbolic
1/sqrt(-4*z + 1)
sage: derivative(C, z, 2) # needs sage.symbolic
2/(-4*z + 1)^(3/2)
sage: derivative(C, z, 3) # needs sage.symbolic
12/(-4*z + 1)^(5/2)
>>> from sage.all import *
>>> derivative(C, z, Integer(1)) # needs sage.symbolic
1/sqrt(-4*z + 1)
>>> derivative(C, z, Integer(2)) # needs sage.symbolic
2/(-4*z + 1)^(3/2)
>>> derivative(C, z, Integer(3)) # needs sage.symbolic
12/(-4*z + 1)^(5/2)
This suggests the existence of a simple explicit formula, which we will now seek. The following small function returns \(d_n=n! \, c_n\):
sage: def d(n): return derivative(s0, n).subs(z=0)
>>> from sage.all import *
>>> def d(n): return derivative(s0, n).subs(z=Integer(0))
Taking successive quotients:
sage: [ (d(n+1) / d(n)) for n in range(1,17) ] # needs sage.symbolic
[2, 6, 10, 14, 18, 22, 26, 30, 34, 38, 42, 46, 50, 54, 58, 62]
>>> from sage.all import *
>>> [ (d(n+Integer(1)) / d(n)) for n in range(Integer(1),Integer(17)) ] # needs sage.symbolic
[2, 6, 10, 14, 18, 22, 26, 30, 34, 38, 42, 46, 50, 54, 58, 62]
we observe that \(d_n\) satisfies the recurrence relation \(d_{n+1}=(4n-2)d_n\), from which we deduce that \(c_n\) satisfies the recurrence relation \(c_{n+1}=\frac{(4n-2)}{n+1}c_n\). Simplifying, we find that \(c_n\) is the \((n-1)\)-th Catalan number:
We check this:
sage: n = var('n') # needs sage.symbolic
sage: c = 1/n*binomial(2*(n-1),n-1) # needs sage.symbolic
sage: [c.subs(n=k) for k in range(1, 11)] # needs sage.symbolic
[1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862]
sage: [catalan_number(k-1) for k in range(1, 11)]
[1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862]
>>> from sage.all import *
>>> n = var('n') # needs sage.symbolic
>>> c = Integer(1)/n*binomial(Integer(2)*(n-Integer(1)),n-Integer(1)) # needs sage.symbolic
>>> [c.subs(n=k) for k in range(Integer(1), Integer(11))] # needs sage.symbolic
[1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862]
>>> [catalan_number(k-Integer(1)) for k in range(Integer(1), Integer(11))]
[1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862]
We can now calculate coefficients much further; here we calculate \(c_{100000}\) which has more than \(60000\) digits:
sage: cc = c(n=100000) # needs sage.symbolic
>>> from sage.all import *
>>> cc = c(n=Integer(100000)) # needs sage.symbolic
This takes a couple of seconds:
sage: %time cc = c(100000) # not tested # needs sage.symbolic
CPU times: user 2.34 s, sys: 0.00 s, total: 2.34 s
Wall time: 2.34 s
sage: ZZ(cc).ndigits() # needs sage.symbolic
60198
>>> from sage.all import *
>>> %time cc = c(Integer(100000)) # not tested # needs sage.symbolic
CPU times: user 2.34 s, sys: 0.00 s, total: 2.34 s
Wall time: 2.34 s
>>> ZZ(cc).ndigits() # needs sage.symbolic
60198
The methods which we have used generalize to all recursively defined
objects: the system of set-theoretic equations can be translated into a
system of equations on the generating function, which enables the
recursive calculation of its coefficients. If the set-theoretic
equations are simple enough (for example, if they only involve Cartesian
products and disjoint unions), the equation for \(C(z)\) is
algebraic. This equation has, in general, no closed-form solution.
However, using confinement, one can deduce a linear differential
equation which \(C(z)\) satisfies. This differential equation, in
turn, can be translated into a recurrence relation of fixed length on
its coefficients \(c_n\). In this case, the series is called
D-finite. After the initial calculation of this recurrence relation,
the calculation of coefficients is very fast. All these steps are purely
algorithmic, and it is planned to port into Sage the implementations
which exist in Maple (the gfun and combstruct packages) or
MuPAD-Combinat (the decomposableObjects library).
For the moment, we illustrate this general procedure in the case of complete binary trees. The generating function \(C(z)\) is a solution to an algebraic equation \(P(z,C(z)) = 0\), where \(P=P(x,y)\) is a polynomial with coefficients in \(\QQ\). In the present case, \(P=y^2-y+x\). We formally differentiate this equation with respect to \(z\):
sage: # needs sage.symbolic
sage: x, y, z = var('x, y, z')
sage: P = function('P')(x, y)
sage: C = function('C')(z)
sage: equation = P(x=z, y=C) == 0
sage: diff(equation, z)
diff(C(z), z)*D[1](P)(z, C(z)) + D[0](P)(z, C(z)) == 0
>>> from sage.all import *
>>> # needs sage.symbolic
>>> x, y, z = var('x, y, z')
>>> P = function('P')(x, y)
>>> C = function('C')(z)
>>> equation = P(x=z, y=C) == Integer(0)
>>> diff(equation, z)
diff(C(z), z)*D[1](P)(z, C(z)) + D[0](P)(z, C(z)) == 0
or, in a more readable format,
From this we deduce:
In the case of complete binary trees, this gives:
sage: P = y^2 - y + x # needs sage.symbolic
sage: Px = diff(P, x); Py = diff(P, y) # needs sage.symbolic
sage: - Px / Py # needs sage.symbolic
-1/(2*y - 1)
>>> from sage.all import *
>>> P = y**Integer(2) - y + x # needs sage.symbolic
>>> Px = diff(P, x); Py = diff(P, y) # needs sage.symbolic
>>> - Px / Py # needs sage.symbolic
-1/(2*y - 1)
Recall that \(P(z, C(z))=0\). Thus, we can calculate this fraction mod \(P\) and, in this way, express the derivative of \(C(z)\) as a polynomial in \(C(z)\) with coefficients in \(\QQ(z)\). In order to achieve this, we construct the quotient ring \(R= \QQ(x)[y]/ (P)\):
sage: Qx = QQ['x'].fraction_field()
sage: Qxy = Qx['y']
sage: R = Qxy.quo(P); R # needs sage.symbolic
Univariate Quotient Polynomial Ring in ybar
over Fraction Field of Univariate Polynomial Ring in x
over Rational Field with modulus y^2 - y + x
>>> from sage.all import *
>>> Qx = QQ['x'].fraction_field()
>>> Qxy = Qx['y']
>>> R = Qxy.quo(P); R # needs sage.symbolic
Univariate Quotient Polynomial Ring in ybar
over Fraction Field of Univariate Polynomial Ring in x
over Rational Field with modulus y^2 - y + x
Note: ybar is the name of the variable \(y\) in the quotient ring.
Todo
add link to some tutorial on quotient rings
We continue the calculation of this fraction in \(R\):
sage: fraction = - R(Px) / R(Py); fraction # needs sage.symbolic
(1/2/(x - 1/4))*ybar - 1/4/(x - 1/4)
>>> from sage.all import *
>>> fraction = - R(Px) / R(Py); fraction # needs sage.symbolic
(1/2/(x - 1/4))*ybar - 1/4/(x - 1/4)
Note
The following variant does not work yet:
sage: fraction = R( - Px / Py ); fraction # todo: not implemented
Traceback (most recent call last):
...
TypeError: denominator must be a unit
>>> from sage.all import *
>>> fraction = R( - Px / Py ); fraction # todo: not implemented
Traceback (most recent call last):
...
TypeError: denominator must be a unit
We lift the result to \(\QQ(x)[y]\) and then substitute \(z\) and \(C(z)\) to obtain an expression for \(\frac{d}{dz}C(z)\):
sage: fraction = fraction.lift(); fraction # needs sage.symbolic
(1/2/(x - 1/4))*y - 1/4/(x - 1/4)
sage: fraction(x=z, y=C) # needs sage.symbolic
2*C(z)/(4*z - 1) - 1/(4*z - 1)
>>> from sage.all import *
>>> fraction = fraction.lift(); fraction # needs sage.symbolic
(1/2/(x - 1/4))*y - 1/4/(x - 1/4)
>>> fraction(x=z, y=C) # needs sage.symbolic
2*C(z)/(4*z - 1) - 1/(4*z - 1)
or, more legibly,
In this simple case, we can directly deduce from this expression a linear differential equation with coefficients in \(\QQ[z]\):
sage: # needs sage.symbolic
sage: equadiff = diff(C,z) == fraction(x=z, y=C)
sage: equadiff
diff(C(z), z) == 2*C(z)/(4*z - 1) - 1/(4*z - 1)
sage: equadiff = equadiff.simplify_rational()
sage: equadiff = equadiff * equadiff.rhs().denominator()
sage: equadiff = equadiff - equadiff.rhs()
sage: equadiff
(4*z - 1)*diff(C(z), z) - 2*C(z) + 1 == 0
>>> from sage.all import *
>>> # needs sage.symbolic
>>> equadiff = diff(C,z) == fraction(x=z, y=C)
>>> equadiff
diff(C(z), z) == 2*C(z)/(4*z - 1) - 1/(4*z - 1)
>>> equadiff = equadiff.simplify_rational()
>>> equadiff = equadiff * equadiff.rhs().denominator()
>>> equadiff = equadiff - equadiff.rhs()
>>> equadiff
(4*z - 1)*diff(C(z), z) - 2*C(z) + 1 == 0
or, more legibly,
It is trivial to verify this equation on the closed form:
sage: Cf = sage.symbolic.function_factory.function('C') # needs sage.symbolic
sage: equadiff.substitute_function(Cf, s0.function(z)) # needs sage.symbolic
(4*z - 1)/sqrt(-4*z + 1) + sqrt(-4*z + 1) == 0
sage: bool(equadiff.substitute_function(Cf, s0.function(z))) # needs sage.symbolic
True
>>> from sage.all import *
>>> Cf = sage.symbolic.function_factory.function('C') # needs sage.symbolic
>>> equadiff.substitute_function(Cf, s0.function(z)) # needs sage.symbolic
(4*z - 1)/sqrt(-4*z + 1) + sqrt(-4*z + 1) == 0
>>> bool(equadiff.substitute_function(Cf, s0.function(z))) # needs sage.symbolic
True
In the general case, one continues to calculate successive derivatives of \(C(z)\). These derivatives are confined in the quotient ring \(\QQ(z)[C]/(P)\) which is of finite dimension \(\deg P\) over \(\QQ(z)\). Therefore, one will eventually find a linear relation among the first \(\deg P\) derivatives of \(C(z)\). Putting it over a single denominator, we obtain a linear differential equation of degree \(\leq \deg P\) with coefficients in \(\QQ[z]\). By extracting the coefficient of \(z^n\) in the differential equation, we obtain the desired recurrence relation on the coefficients; in this case we recover the relation we had already found, based on the closed form:
After fixing the correct initial conditions, it becomes possible to calculate the coefficients of \(C(z)\) recursively:
sage: def C(n): return 1 if n <= 1 else (4*n-6)/n * C(n-1)
sage: [ C(i) for i in range(10) ]
[1, 1, 1, 2, 5, 14, 42, 132, 429, 1430]
>>> from sage.all import *
>>> def C(n): return Integer(1) if n <= Integer(1) else (Integer(4)*n-Integer(6))/n * C(n-Integer(1))
>>> [ C(i) for i in range(Integer(10)) ]
[1, 1, 1, 2, 5, 14, 42, 132, 429, 1430]
If \(n\) is too large for the explicit calculation of \(c_n\), a sequence asymptotically equivalent to the sequence of coefficients \(c_n\) may be sought. Here again, there are generic techniques. The central tool is complex analysis, specifically, the study of the generating function around its singularities. In the present instance, the singularity is at \(z_0=1/4\) and one would obtain \(c_n \sim \frac{4^n}{n^{3/2}\sqrt{\pi}}\).
Summary¶
We see here a general phenomenon of computer algebra: the best data structure to describe a complicated mathematical object (a real number, a sequence, a formal power series, a function, a set) is often an equation defining the object (or a system of equations, typically with some initial conditions). Attempting to find a closed-form solution to this equation is not necessarily of interest: on the one hand, such a closed form rarely exists (e.g., the problem of solving a polynomial by radicals), and on the other hand, the equation, in itself, contains all the necessary information to calculate algorithmically the properties of the object under consideration (e.g., a numerical approximation, the initial terms or elements, an asymptotic equivalent), or to calculate with the object itself (e.g., performing arithmetic on power series). Therefore, instead of solving the equation, we look for the equation describing the object which is best suited to the problem we want to solve.
As we saw in our example, confinement (for example, in a finite dimensional vector space) is a fundamental tool for studying such equations. This notion of confinement is widely applicable in elimination techniques (linear algebra, Gröbner bases, and their algebro-differential generalizations). The same tool is central in algorithms for automatic summation and automatic verification of identities (Gosper’s algorithm, Zeilberger’s algorithm, and their generalizations; see also Exercise: alternating sign matrices).
Todo
add link to some tutorial on summation
All these techniques and their many generalizations are at the heart of
very active topics of research: automatic combinatorics and analytic
combinatorics, with major applications in the analysis of algorithms. It is
likely, and desirable, that they will be progressively implemented in
Sage.
Common enumerated sets¶
First example: the subsets of a set¶
Fix a set \(E\) of size \(n\) and consider the subsets of
\(E\) of size \(k\). We know that these subsets are counted
by the binomial coefficients \(\binom n k\). We can therefore
calculate the number of subsets of size \(k=2\) of
\(E=\{1,2,3,4\}\) with the function binomial:
sage: binomial(4, 2)
6
>>> from sage.all import *
>>> binomial(Integer(4), Integer(2))
6
Alternatively, we can construct the set \(\mathcal P_2(E)\) of all the subsets of size \(2\) of \(E\), then ask its cardinality:
sage: S = Subsets([1,2,3,4], 2)
sage: S.cardinality()
6
>>> from sage.all import *
>>> S = Subsets([Integer(1),Integer(2),Integer(3),Integer(4)], Integer(2))
>>> S.cardinality()
6
Once S has been constructed, we can also obtain the list of its
elements:
sage: S.list()
[{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}]
>>> from sage.all import *
>>> S.list()
[{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}]
or select an element at random:
sage: S.random_element() # random
{1, 4}
>>> from sage.all import *
>>> S.random_element() # random
{1, 4}
More precisely, the object S models the set
\(\mathcal P_2(E)\) equipped with a fixed order (here,
lexicographic order). It is therefore possible to ask for its
\(5\)-th element, keeping in mind that, as with Python lists, the first
element is numbered zero:
sage: S.unrank(4)
{2, 4}
>>> from sage.all import *
>>> S.unrank(Integer(4))
{2, 4}
As a shortcut, in this setting, one can also use the notation:
sage: S[4]
{2, 4}
>>> from sage.all import *
>>> S[Integer(4)]
{2, 4}
but this should be used with care because some sets have a natural indexing other than by \((0, 1, \dots)\).
Conversely, one can calculate the position of an object in this order:
sage: s = S([2,4]); s
{2, 4}
sage: S.rank(s)
4
>>> from sage.all import *
>>> s = S([Integer(2),Integer(4)]); s
{2, 4}
>>> S.rank(s)
4
Note that S is not the list of its elements. One can, for example,
model the set \(\mathcal P(\mathcal P(\mathcal P(E)))\) and
calculate its cardinality (\(2^{2^{2^4}}\)):
sage: E = Set([1,2,3,4])
sage: S = Subsets(Subsets(Subsets(E))); S
Subsets of Subsets of Subsets of {1, 2, 3, 4}
sage: n = S.cardinality(); n
2003529930406846464979072351560255750447825475569751419265016973...
>>> from sage.all import *
>>> E = Set([Integer(1),Integer(2),Integer(3),Integer(4)])
>>> S = Subsets(Subsets(Subsets(E))); S
Subsets of Subsets of Subsets of {1, 2, 3, 4}
>>> n = S.cardinality(); n
2003529930406846464979072351560255750447825475569751419265016973...
which is roughly \(2\cdot 10^{19728}\):
sage: n.ndigits()
19729
>>> from sage.all import *
>>> n.ndigits()
19729
or ask for its \(237102124\)-th element:
sage: S.unrank(237102123) # random print output
{{{2, 4}, {1, 4}, {}, {1, 3, 4}, {1, 2, 4}, {4}, {2, 3}, {1, 3}, {2}},
{{1, 3}, {2, 4}, {1, 2, 4}, {}, {3, 4}}}
>>> from sage.all import *
>>> S.unrank(Integer(237102123)) # random print output
{{{2, 4}, {1, 4}, {}, {1, 3, 4}, {1, 2, 4}, {4}, {2, 3}, {1, 3}, {2}},
{{1, 3}, {2, 4}, {1, 2, 4}, {}, {3, 4}}}
It would be physically impossible to construct explicitly all the elements of \(S\), as there are many more of them than there are particles in the universe (estimated at \(10^{82}\)).
Remark: it would be natural in Python to use len(S) to ask for the
cardinality of S. This is not possible because Python requires that the
result of len be an integer of type int; this could cause
overflows, and would not permit the return of {Infinity} for infinite
sets:
sage: len(S)
Traceback (most recent call last):
...
OverflowError: cannot fit 'int' into an index-sized integer
>>> from sage.all import *
>>> len(S)
Traceback (most recent call last):
...
OverflowError: cannot fit 'int' into an index-sized integer
Partitions of integers¶
We now consider another classic problem: given a positive integer \(n\), in how many ways can it be written in the form of a sum \(n=i_1+i_2+\dots+i_\ell\), where \(i_1,\dots,i_\ell\) are positive integers? There are two cases to distinguish:
the order of the elements in the sum is not important, in which case we call \((i_1,\dots,i_\ell)\) a partition of \(n\);
the order of the elements in the sum is important, in which case we call \((i_1,\dots,i_\ell)\) a composition of \(n\).
We will begin with the partitions of \(n=5\); as before, we begin by constructing the set of these partitions:
sage: P5 = Partitions(5); P5
Partitions of the integer 5
>>> from sage.all import *
>>> P5 = Partitions(Integer(5)); P5
Partitions of the integer 5
then we ask for its cardinality:
sage: P5.cardinality()
7
>>> from sage.all import *
>>> P5.cardinality()
7
We look at these \(7\) partitions; the order being irrelevant, the entries are ordered, by convention, in decreasing order.
sage: P5.list()
[[5], [4, 1], [3, 2], [3, 1, 1], [2, 2, 1], [2, 1, 1, 1],
[1, 1, 1, 1, 1]]
>>> from sage.all import *
>>> P5.list()
[[5], [4, 1], [3, 2], [3, 1, 1], [2, 2, 1], [2, 1, 1, 1],
[1, 1, 1, 1, 1]]
The calculation of the number of partitions uses the Rademacher
formula (Wikipedia article Partition_(number_theory)), implemented in C
and highly optimized, which makes it very fast:
sage: Partitions(100000).cardinality()
27493510569775696512677516320986352688173429315980054758203125984302147328114964173055050741660736621590157844774296248940493063070200461792764493033510116079342457190155718943509725312466108452006369558934464248716828789832182345009262853831404597021307130674510624419227311238999702284408609370935531629697851569569892196108480158600569421098519
>>> from sage.all import *
>>> Partitions(Integer(100000)).cardinality()
27493510569775696512677516320986352688173429315980054758203125984302147328114964173055050741660736621590157844774296248940493063070200461792764493033510116079342457190155718943509725312466108452006369558934464248716828789832182345009262853831404597021307130674510624419227311238999702284408609370935531629697851569569892196108480158600569421098519
Partitions of integers are combinatorial objects naturally equipped with many operations. They are therefore returned as objects that are richer than simple lists:
sage: P7 = Partitions(7)
sage: p = P7.unrank(5); p
[4, 2, 1]
sage: type(p)
<class 'sage.combinat.partition.Partitions_n_with_category.element_class'>
>>> from sage.all import *
>>> P7 = Partitions(Integer(7))
>>> p = P7.unrank(Integer(5)); p
[4, 2, 1]
>>> type(p)
<class 'sage.combinat.partition.Partitions_n_with_category.element_class'>
For example, they can be represented graphically by a Ferrers diagram:
sage: print(p.ferrers_diagram())
****
**
*
>>> from sage.all import *
>>> print(p.ferrers_diagram())
****
**
*
We leave it to the user to explore by introspection the available operations.
Note that we can also construct a partition directly by:
sage: Partition([4,2,1])
[4, 2, 1]
>>> from sage.all import *
>>> Partition([Integer(4),Integer(2),Integer(1)])
[4, 2, 1]
or:
sage: P7([4,2,1])
[4, 2, 1]
>>> from sage.all import *
>>> P7([Integer(4),Integer(2),Integer(1)])
[4, 2, 1]
If one wants to restrict the possible values of the parts
\(i_1,\dots,i_\ell\) of the partition as, for example, when giving
change, one can use WeightedIntegerVectors. For example, the
following calculation:
sage: WeightedIntegerVectors(8, [2,3,5]).list()
[[0, 1, 1], [1, 2, 0], [4, 0, 0]]
>>> from sage.all import *
>>> WeightedIntegerVectors(Integer(8), [Integer(2),Integer(3),Integer(5)]).list()
[[0, 1, 1], [1, 2, 0], [4, 0, 0]]
shows that to make 8 dollars using 2, 3, and 5 dollar bills, one can use a 3 and a 5 dollar bill, or a 2 and two 3 dollar bills, or four 2 dollar bills.
Compositions of integers are manipulated the same way:
sage: C5 = Compositions(5); C5
Compositions of 5
sage: C5.cardinality()
16
sage: C5.list()
[[1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 1, 2, 1], [1, 1, 3],
[1, 2, 1, 1], [1, 2, 2], [1, 3, 1], [1, 4], [2, 1, 1, 1],
[2, 1, 2], [2, 2, 1], [2, 3], [3, 1, 1], [3, 2], [4, 1], [5]]
>>> from sage.all import *
>>> C5 = Compositions(Integer(5)); C5
Compositions of 5
>>> C5.cardinality()
16
>>> C5.list()
[[1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 1, 2, 1], [1, 1, 3],
[1, 2, 1, 1], [1, 2, 2], [1, 3, 1], [1, 4], [2, 1, 1, 1],
[2, 1, 2], [2, 2, 1], [2, 3], [3, 1, 1], [3, 2], [4, 1], [5]]
The number \(16\) above seems significant and suggests the existence of a formula. We look at the number of compositions of \(n\) ranging from \(0\) to \(9\):
sage: [Compositions(n).cardinality() for n in range(10)]
[1, 1, 2, 4, 8, 16, 32, 64, 128, 256]
>>> from sage.all import *
>>> [Compositions(n).cardinality() for n in range(Integer(10))]
[1, 1, 2, 4, 8, 16, 32, 64, 128, 256]
Similarly, if we consider the number of compositions of \(5\) by length, we find a line of Pascal’s triangle:
sage: x = var('x') # needs sage.symbolic
sage: sum(x^len(c) for c in C5) # needs sage.symbolic
x^5 + 4*x^4 + 6*x^3 + 4*x^2 + x
>>> from sage.all import *
>>> x = var('x') # needs sage.symbolic
>>> sum(x**len(c) for c in C5) # needs sage.symbolic
x^5 + 4*x^4 + 6*x^3 + 4*x^2 + x
The above example uses a functionality which we have not seen yet:
C5 being iterable, it can be used like a list in a for loop or
a comprehension (Set comprehension and iterators).
Prove the formulas suggested by the above examples for the number of compositions of \(n\) and the number of compositions of \(n\) of length \(k\); investigate by introspection whether
Sageuses these formulas for calculating cardinalities.
Some other finite enumerated sets¶
Essentially, the principle is the same for all the finite sets with
which one wants to do combinatorics in Sage; begin by constructing
an object which models this set, and then supply appropriate methods,
following a uniform interface [1]. We now give a few more typical
examples.
Intervals of integers:
sage: C = IntegerRange(3, 21, 2); C
{3, 5, ..., 19}
sage: C.cardinality()
9
sage: C.list()
[3, 5, 7, 9, 11, 13, 15, 17, 19]
>>> from sage.all import *
>>> C = IntegerRange(Integer(3), Integer(21), Integer(2)); C
{3, 5, ..., 19}
>>> C.cardinality()
9
>>> C.list()
[3, 5, 7, 9, 11, 13, 15, 17, 19]
Permutations:
sage: C = Permutations(4); C
Standard permutations of 4
sage: C.cardinality()
24
sage: C.list()
[[1, 2, 3, 4], [1, 2, 4, 3], [1, 3, 2, 4], [1, 3, 4, 2],
[1, 4, 2, 3], [1, 4, 3, 2], [2, 1, 3, 4], [2, 1, 4, 3],
[2, 3, 1, 4], [2, 3, 4, 1], [2, 4, 1, 3], [2, 4, 3, 1],
[3, 1, 2, 4], [3, 1, 4, 2], [3, 2, 1, 4], [3, 2, 4, 1],
[3, 4, 1, 2], [3, 4, 2, 1], [4, 1, 2, 3], [4, 1, 3, 2],
[4, 2, 1, 3], [4, 2, 3, 1], [4, 3, 1, 2], [4, 3, 2, 1]]
>>> from sage.all import *
>>> C = Permutations(Integer(4)); C
Standard permutations of 4
>>> C.cardinality()
24
>>> C.list()
[[1, 2, 3, 4], [1, 2, 4, 3], [1, 3, 2, 4], [1, 3, 4, 2],
[1, 4, 2, 3], [1, 4, 3, 2], [2, 1, 3, 4], [2, 1, 4, 3],
[2, 3, 1, 4], [2, 3, 4, 1], [2, 4, 1, 3], [2, 4, 3, 1],
[3, 1, 2, 4], [3, 1, 4, 2], [3, 2, 1, 4], [3, 2, 4, 1],
[3, 4, 1, 2], [3, 4, 2, 1], [4, 1, 2, 3], [4, 1, 3, 2],
[4, 2, 1, 3], [4, 2, 3, 1], [4, 3, 1, 2], [4, 3, 2, 1]]
Set partitions:
sage: C = SetPartitions(["a", "b", "c"])
sage: C # random print output
Set partitions of {'a', 'c', 'b'}
sage: C.cardinality()
5
sage: C.list()
[{{'a', 'b', 'c'}},
{{'a', 'b'}, {'c'}},
{{'a', 'c'}, {'b'}},
{{'a'}, {'b', 'c'}},
{{'a'}, {'b'}, {'c'}}]
>>> from sage.all import *
>>> C = SetPartitions(["a", "b", "c"])
>>> C # random print output
Set partitions of {'a', 'c', 'b'}
>>> C.cardinality()
5
>>> C.list()
[{{'a', 'b', 'c'}},
{{'a', 'b'}, {'c'}},
{{'a', 'c'}, {'b'}},
{{'a'}, {'b', 'c'}},
{{'a'}, {'b'}, {'c'}}]
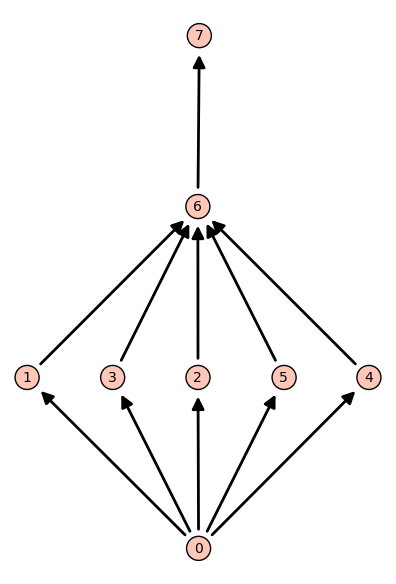
Partial orders on a set of \(8\) elements, up to isomorphism:
sage: C = Posets(7); C
Posets containing 7 elements
sage: C.cardinality()
2045
>>> from sage.all import *
>>> C = Posets(Integer(7)); C
Posets containing 7 elements
>>> C.cardinality()
2045
sage: C.unrank(20).plot()
Graphics object consisting of ... graphics primitives
>>> from sage.all import *
>>> C.unrank(Integer(20)).plot()
Graphics object consisting of ... graphics primitives
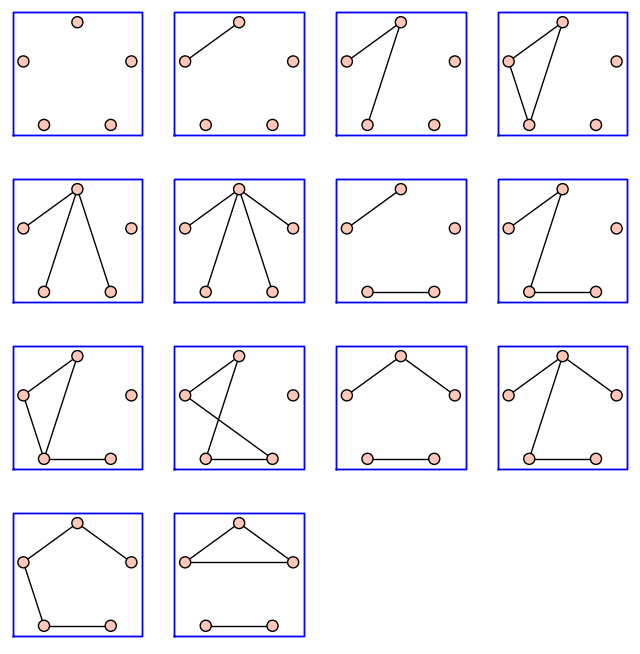
One can iterate through all graphs up to isomorphism. For example, there are 34 simple graphs with 5 vertices:
sage: len(list(graphs(5)))
34
>>> from sage.all import *
>>> len(list(graphs(Integer(5))))
34
Here are those with at most \(4\) edges:
sage: up_to_four_edges = list(graphs(5, lambda G: G.size() <= 4))
sage: pretty_print(*up_to_four_edges)
>>> from sage.all import *
>>> up_to_four_edges = list(graphs(Integer(5), lambda G: G.size() <= Integer(4)))
>>> pretty_print(*up_to_four_edges)
However, the set C of these graphs is not yet available in
Sage; as a result, the following commands are not yet
implemented:
sage: # not implemented
sage: C = Graphs(5)
sage: C.cardinality()
34
sage: Graphs(19).cardinality()
24637809253125004524383007491432768
sage: Graphs(19).random_element()
Graph on 19 vertices
>>> from sage.all import *
>>> # not implemented
>>> C = Graphs(Integer(5))
>>> C.cardinality()
34
>>> Graphs(Integer(19)).cardinality()
24637809253125004524383007491432768
>>> Graphs(Integer(19)).random_element()
Graph on 19 vertices
What we have seen so far also applies, in principle, to finite algebraic structures like the dihedral groups:
sage: G = DihedralGroup(4); G
Dihedral group of order 8 as a permutation group
sage: G.cardinality()
8
sage: G.list()
[(), (1,3)(2,4), (1,4,3,2), (1,2,3,4), (2,4), (1,3), (1,4)(2,3), (1,2)(3,4)]
>>> from sage.all import *
>>> G = DihedralGroup(Integer(4)); G
Dihedral group of order 8 as a permutation group
>>> G.cardinality()
8
>>> G.list()
[(), (1,3)(2,4), (1,4,3,2), (1,2,3,4), (2,4), (1,3), (1,4)(2,3), (1,2)(3,4)]
or the algebra of \(2\times 2\) matrices over the finite field \(\ZZ/2\ZZ\):
sage: C = MatrixSpace(GF(2), 2) # needs sage.modules sage.rings.finite_rings
sage: C.list() # needs sage.modules sage.rings.finite_rings
[
[0 0] [1 0] [0 1] [0 0] [0 0] [1 1] [1 0] [1 0] [0 1] [0 1]
[0 0], [0 0], [0 0], [1 0], [0 1], [0 0], [1 0], [0 1], [1 0], [0 1],
[0 0] [1 1] [1 1] [1 0] [0 1] [1 1]
[1 1], [1 0], [0 1], [1 1], [1 1], [1 1]
]
sage: C.cardinality() # needs sage.modules sage.rings.finite_rings
16
>>> from sage.all import *
>>> C = MatrixSpace(GF(Integer(2)), Integer(2)) # needs sage.modules sage.rings.finite_rings
>>> C.list() # needs sage.modules sage.rings.finite_rings
[
[0 0] [1 0] [0 1] [0 0] [0 0] [1 1] [1 0] [1 0] [0 1] [0 1]
[0 0], [0 0], [0 0], [1 0], [0 1], [0 0], [1 0], [0 1], [1 0], [0 1],
<BLANKLINE>
[0 0] [1 1] [1 1] [1 0] [0 1] [1 1]
[1 1], [1 0], [0 1], [1 1], [1 1], [1 1]
]
>>> C.cardinality() # needs sage.modules sage.rings.finite_rings
16
Set comprehension and iterators¶
We will now show some of the possibilities offered by Python for
constructing (and iterating through) sets, with a notation that is
flexible and close to usual mathematical usage, and in particular the
benefits this yields in combinatorics.
We begin by constructing the finite set \(\{i^2\ \|\ i \in \{1,3,7\}\}\):
sage: [ i^2 for i in [1, 3, 7] ]
[1, 9, 49]
>>> from sage.all import *
>>> [ i**Integer(2) for i in [Integer(1), Integer(3), Integer(7)] ]
[1, 9, 49]
and then the same set, but with \(i\) running from \(1\) to \(9\):
sage: [ i^2 for i in range(1,10) ]
[1, 4, 9, 16, 25, 36, 49, 64, 81]
>>> from sage.all import *
>>> [ i**Integer(2) for i in range(Integer(1),Integer(10)) ]
[1, 4, 9, 16, 25, 36, 49, 64, 81]
A construction of this form in Python is called set comprehension.
A clause can be added to keep only those elements with \(i\) prime:
sage: [ i^2 for i in range(1,10) if is_prime(i) ]
[4, 9, 25, 49]
>>> from sage.all import *
>>> [ i**Integer(2) for i in range(Integer(1),Integer(10)) if is_prime(i) ]
[4, 9, 25, 49]
Combining more than one set comprehension, it is possible to construct the set \(\{(i,j) \ | \ 1\leq j < i <5\}\):
sage: [ (i,j) for i in range(1,6) for j in range(1,i) ]
[(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3),
(5, 1), (5, 2), (5, 3), (5, 4)]
>>> from sage.all import *
>>> [ (i,j) for i in range(Integer(1),Integer(6)) for j in range(Integer(1),i) ]
[(2, 1), (3, 1), (3, 2), (4, 1), (4, 2), (4, 3),
(5, 1), (5, 2), (5, 3), (5, 4)]
or to produce Pascal’s triangle:
sage: [[binomial(n,i) for i in range(n+1)] for n in range(10)]
[[1],
[1, 1],
[1, 2, 1],
[1, 3, 3, 1],
[1, 4, 6, 4, 1],
[1, 5, 10, 10, 5, 1],
[1, 6, 15, 20, 15, 6, 1],
[1, 7, 21, 35, 35, 21, 7, 1],
[1, 8, 28, 56, 70, 56, 28, 8, 1],
[1, 9, 36, 84, 126, 126, 84, 36, 9, 1]]
>>> from sage.all import *
>>> [[binomial(n,i) for i in range(n+Integer(1))] for n in range(Integer(10))]
[[1],
[1, 1],
[1, 2, 1],
[1, 3, 3, 1],
[1, 4, 6, 4, 1],
[1, 5, 10, 10, 5, 1],
[1, 6, 15, 20, 15, 6, 1],
[1, 7, 21, 35, 35, 21, 7, 1],
[1, 8, 28, 56, 70, 56, 28, 8, 1],
[1, 9, 36, 84, 126, 126, 84, 36, 9, 1]]
The execution of a set comprehension is accomplished in two steps; first
an iterator is constructed, and then a list is filled with the
elements successively produced by the iterator. Technically, an
iterator is an object with a method next which returns a new value
each time it is called, until it is exhausted. For example, the
following iterator it:
sage: it = (binomial(3, i) for i in range(4))
>>> from sage.all import *
>>> it = (binomial(Integer(3), i) for i in range(Integer(4)))
returns successively the binomial coefficients \(\binom 3 i\) with \(i=0,1,2,3\):
sage: next(it)
1
sage: next(it)
3
sage: next(it)
3
sage: next(it)
1
>>> from sage.all import *
>>> next(it)
1
>>> next(it)
3
>>> next(it)
3
>>> next(it)
1
When the iterator is finally exhausted, an exception is raised:
sage: next(it)
Traceback (most recent call last):
...
StopIteration
>>> from sage.all import *
>>> next(it)
Traceback (most recent call last):
...
StopIteration
More generally, an iterable is a Python object L (a list,
a set, …) over whose elements it is possible to iterate. Technically,
the iterator is constructed by iter(L). In practice, the commands
iter and next are used very rarely, since for loops and list
comprehensions provide a much pleasanter syntax:
sage: for s in Subsets(3):
....: print(s)
{}
{1}
{2}
{3}
{1, 2}
{1, 3}
{2, 3}
{1, 2, 3}
>>> from sage.all import *
>>> for s in Subsets(Integer(3)):
... print(s)
{}
{1}
{2}
{3}
{1, 2}
{1, 3}
{2, 3}
{1, 2, 3}
sage: [ s.cardinality() for s in Subsets(3) ]
[0, 1, 1, 1, 2, 2, 2, 3]
>>> from sage.all import *
>>> [ s.cardinality() for s in Subsets(Integer(3)) ]
[0, 1, 1, 1, 2, 2, 2, 3]
What is the point of an iterator? Consider the following example:
sage: sum( [ binomial(8, i) for i in range(9) ] )
256
>>> from sage.all import *
>>> sum( [ binomial(Integer(8), i) for i in range(Integer(9)) ] )
256
When it is executed, a list of \(9\) elements is constructed, and
then it is passed as an argument to sum to add them up. If, on the
other hand, the iterator is passed directly to sum (note the absence
of square brackets):
sage: sum( binomial(8, i) for i in range(9) )
256
>>> from sage.all import *
>>> sum( binomial(Integer(8), i) for i in range(Integer(9)) )
256
the function sum receives the iterator directly, and can
short-circuit the construction of the intermediate list. If there are a
large number of elements, this avoids allocating a large quantity of
memory to fill a list which will be immediately destroyed.
Most functions that take a list of elements as input will also accept an iterator (or an iterable) instead. To begin with, one can obtain the list (or the tuple) of elements of an iterator as follows:
sage: list(binomial(8, i) for i in range(9))
[1, 8, 28, 56, 70, 56, 28, 8, 1]
sage: tuple(binomial(8, i) for i in range(9))
(1, 8, 28, 56, 70, 56, 28, 8, 1)
>>> from sage.all import *
>>> list(binomial(Integer(8), i) for i in range(Integer(9)))
[1, 8, 28, 56, 70, 56, 28, 8, 1]
>>> tuple(binomial(Integer(8), i) for i in range(Integer(9)))
(1, 8, 28, 56, 70, 56, 28, 8, 1)
We now consider the functions all and any which denote
respectively the \(n\)-ary and and or:
sage: all([True, True, True, True])
True
sage: all([True, False, True, True])
False
sage: any([False, False, False, False])
False
sage: any([False, False, True, False])
True
>>> from sage.all import *
>>> all([True, True, True, True])
True
>>> all([True, False, True, True])
False
>>> any([False, False, False, False])
False
>>> any([False, False, True, False])
True
The following example verifies that all primes from \(3\) to \(99\) are odd:
sage: all( is_odd(p) for p in range(3,100) if is_prime(p) )
True
>>> from sage.all import *
>>> all( is_odd(p) for p in range(Integer(3),Integer(100)) if is_prime(p) )
True
A Mersenne prime is a prime of the form \(2^p -1\). We verify that, for \(p<1000\), if \(2^p-1\) is prime, then \(p\) is also prime:
sage: def mersenne(p): return 2^p -1
sage: [ is_prime(p)
....: for p in range(1000) if is_prime(mersenne(p)) ]
[True, True, True, True, True, True, True, True, True, True,
True, True, True, True]
>>> from sage.all import *
>>> def mersenne(p): return Integer(2)**p -Integer(1)
>>> [ is_prime(p)
... for p in range(Integer(1000)) if is_prime(mersenne(p)) ]
[True, True, True, True, True, True, True, True, True, True,
True, True, True, True]
Is the converse true?
We now try to find the smallest counter-example. In order to do this, we
use the Sage function exists:
sage: exists( (p for p in range(1000) if is_prime(p)),
....: lambda p: not is_prime(mersenne(p)) )
(True, 11)
>>> from sage.all import *
>>> exists( (p for p in range(Integer(1000)) if is_prime(p)),
... lambda p: not is_prime(mersenne(p)) )
(True, 11)
Alternatively, we could construct an iterator on the counter-examples:
sage: counter_examples = (p for p in range(1000)
....: if is_prime(p) and not is_prime(mersenne(p)))
sage: next(counter_examples)
11
sage: next(counter_examples)
23
>>> from sage.all import *
>>> counter_examples = (p for p in range(Integer(1000))
... if is_prime(p) and not is_prime(mersenne(p)))
>>> next(counter_examples)
11
>>> next(counter_examples)
23
Operations on iterators¶
Python provides numerous tools for manipulating iterators; most of them
are in the itertools library, which can be imported by:
sage: import itertools
>>> from sage.all import *
>>> import itertools
We will demonstrate some applications, taking as a starting point the permutations of \(3\):
sage: list(Permutations(3))
[[1, 2, 3], [1, 3, 2], [2, 1, 3],
[2, 3, 1], [3, 1, 2], [3, 2, 1]]
>>> from sage.all import *
>>> list(Permutations(Integer(3)))
[[1, 2, 3], [1, 3, 2], [2, 1, 3],
[2, 3, 1], [3, 1, 2], [3, 2, 1]]
We can list the elements of a set by numbering them:
sage: list(enumerate(Permutations(3)))
[(0, [1, 2, 3]), (1, [1, 3, 2]), (2, [2, 1, 3]),
(3, [2, 3, 1]), (4, [3, 1, 2]), (5, [3, 2, 1])]
>>> from sage.all import *
>>> list(enumerate(Permutations(Integer(3))))
[(0, [1, 2, 3]), (1, [1, 3, 2]), (2, [2, 1, 3]),
(3, [2, 3, 1]), (4, [3, 1, 2]), (5, [3, 2, 1])]
or select only the elements in positions 2, 3, and 4 (analogue of
l[1:4]):
sage: import itertools
sage: list(itertools.islice(Permutations(3), int(1), int(4)))
[[1, 3, 2], [2, 1, 3], [2, 3, 1]]
>>> from sage.all import *
>>> import itertools
>>> list(itertools.islice(Permutations(Integer(3)), int(Integer(1)), int(Integer(4))))
[[1, 3, 2], [2, 1, 3], [2, 3, 1]]
To apply a function to all the elements, one can do:
sage: [z.cycle_type() for z in Permutations(3)]
[[1, 1, 1], [2, 1], [2, 1], [3], [3], [2, 1]]
>>> from sage.all import *
>>> [z.cycle_type() for z in Permutations(Integer(3))]
[[1, 1, 1], [2, 1], [2, 1], [3], [3], [2, 1]]
and similarly to select the elements satisfying a certain condition:
sage: [z for z in Permutations(3) if z.has_pattern([1,2])]
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2]]
>>> from sage.all import *
>>> [z for z in Permutations(Integer(3)) if z.has_pattern([Integer(1),Integer(2)])]
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2]]
Implementation of new iterators¶
It is easy to construct new iterators, using the keyword yield
instead of return in a function:
sage: def f(n):
....: for i in range(n):
....: yield i
>>> from sage.all import *
>>> def f(n):
... for i in range(n):
... yield i
After the yield, execution is not halted, but only suspended, ready
to be continued from the same point. The result of the function is
therefore an iterator over the successive values returned by yield:
sage: g = f(4)
sage: next(g)
0
sage: next(g)
1
sage: next(g)
2
sage: next(g)
3
>>> from sage.all import *
>>> g = f(Integer(4))
>>> next(g)
0
>>> next(g)
1
>>> next(g)
2
>>> next(g)
3
sage: next(g)
Traceback (most recent call last):
...
StopIteration
>>> from sage.all import *
>>> next(g)
Traceback (most recent call last):
...
StopIteration
The function could be used as follows:
sage: [ x for x in f(5) ]
[0, 1, 2, 3, 4]
>>> from sage.all import *
>>> [ x for x in f(Integer(5)) ]
[0, 1, 2, 3, 4]
This model of computation, called continuation, is very useful in combinatorics, especially when combined with recursion. Here is how to generate all words of a given length on a given alphabet:
sage: def words(alphabet, l):
....: if l == 0:
....: yield []
....: else:
....: for word in words(alphabet, l-1):
....: for l in alphabet:
....: yield word + [l]
sage: [ w for w in words(['a','b'], 3) ]
[['a', 'a', 'a'], ['a', 'a', 'b'], ['a', 'b', 'a'],
['a', 'b', 'b'], ['b', 'a', 'a'], ['b', 'a', 'b'],
['b', 'b', 'a'], ['b', 'b', 'b']]
>>> from sage.all import *
>>> def words(alphabet, l):
... if l == Integer(0):
... yield []
... else:
... for word in words(alphabet, l-Integer(1)):
... for l in alphabet:
... yield word + [l]
>>> [ w for w in words(['a','b'], Integer(3)) ]
[['a', 'a', 'a'], ['a', 'a', 'b'], ['a', 'b', 'a'],
['a', 'b', 'b'], ['b', 'a', 'a'], ['b', 'a', 'b'],
['b', 'b', 'a'], ['b', 'b', 'b']]
These words can then be counted by:
sage: sum(1 for w in words(['a','b','c','d'], 10))
1048576
>>> from sage.all import *
>>> sum(Integer(1) for w in words(['a','b','c','d'], Integer(10)))
1048576
Counting the words one by one is clearly not an efficient method in this case, since the formula \(n^\ell\) is also available; note, though, that this is not the stupidest possible approach - it does, at least, avoid constructing the entire list in memory.
We now consider Dyck words, which are well-parenthesized words in the letters “\((\)” and “\()\)”. The function below generates all the Dyck words of a given length (where the length is the number of pairs of parentheses), using the recursive definition which says that a Dyck word is either empty or of the form \((w_1)w_2\) where \(w_1\) and \(w_2\) are Dyck words:
sage: def dyck_words(l):
....: if l==0:
....: yield ''
....: else:
....: for k in range(l):
....: for w1 in dyck_words(k):
....: for w2 in dyck_words(l-k-1):
....: yield '('+w1+')'+w2
>>> from sage.all import *
>>> def dyck_words(l):
... if l==Integer(0):
... yield ''
... else:
... for k in range(l):
... for w1 in dyck_words(k):
... for w2 in dyck_words(l-k-Integer(1)):
... yield '('+w1+')'+w2
Here are all the Dyck words of length \(4\):
sage: list(dyck_words(4))
['()()()()', '()()(())', '()(())()', '()(()())', '()((()))',
'(())()()', '(())(())', '(()())()', '((()))()', '(()()())',
'(()(()))', '((())())', '((()()))', '(((())))']
>>> from sage.all import *
>>> list(dyck_words(Integer(4)))
['()()()()', '()()(())', '()(())()', '()(()())', '()((()))',
'(())()()', '(())(())', '(()())()', '((()))()', '(()()())',
'(()(()))', '((())())', '((()()))', '(((())))']
Counting them, we recover a well-known sequence:
sage: [ sum(1 for w in dyck_words(l)) for l in range(10) ]
[1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862]
>>> from sage.all import *
>>> [ sum(Integer(1) for w in dyck_words(l)) for l in range(Integer(10)) ]
[1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862]
Constructions¶
We will now see how to construct new sets starting from these building blocks. In fact, we have already begun to do this with the construction of \(\mathcal P(\mathcal P(\mathcal P(\{1,2,3,4\})))\) in the previous section, and to construct the example of sets of cards in Initial examples.
Consider a large Cartesian product:
sage: C = cartesian_product([Compositions(8), Permutations(20)]); C
The Cartesian product of (Compositions of 8, Standard permutations of 20)
sage: C.cardinality()
311411457046609920000
>>> from sage.all import *
>>> C = cartesian_product([Compositions(Integer(8)), Permutations(Integer(20))]); C
The Cartesian product of (Compositions of 8, Standard permutations of 20)
>>> C.cardinality()
311411457046609920000
Clearly, it is impractical to construct the list of all the elements of this Cartesian product! And, in the following example, \(H\) is equipped with the usual combinatorial operations and also its structure as a product group:
sage: G = DihedralGroup(4)
sage: H = cartesian_product([G,G])
sage: H in Groups()
True
sage: H.an_element()
((1,3), (1,3))
sage: t = H([G.gen(0), G.gen(0)])
sage: t
((1,2,3,4), (1,2,3,4))
sage: t*t
((1,3)(2,4), (1,3)(2,4))
>>> from sage.all import *
>>> G = DihedralGroup(Integer(4))
>>> H = cartesian_product([G,G])
>>> H in Groups()
True
>>> H.an_element()
((1,3), (1,3))
>>> t = H([G.gen(Integer(0)), G.gen(Integer(0))])
>>> t
((1,2,3,4), (1,2,3,4))
>>> t*t
((1,3)(2,4), (1,3)(2,4))
We now construct the union of two existing disjoint sets:
sage: C = DisjointUnionEnumeratedSets(
....: [ Compositions(4), Permutations(3)] )
sage: C
Disjoint union of Family (Compositions of 4,
Standard permutations of 3)
sage: C.cardinality()
14
sage: C.list()
[[1, 1, 1, 1], [1, 1, 2], [1, 2, 1], [1, 3], [2, 1, 1], [2, 2],
[3, 1], [4], [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1],
[3, 1, 2], [3, 2, 1]]
>>> from sage.all import *
>>> C = DisjointUnionEnumeratedSets(
... [ Compositions(Integer(4)), Permutations(Integer(3))] )
>>> C
Disjoint union of Family (Compositions of 4,
Standard permutations of 3)
>>> C.cardinality()
14
>>> C.list()
[[1, 1, 1, 1], [1, 1, 2], [1, 2, 1], [1, 3], [2, 1, 1], [2, 2],
[3, 1], [4], [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1],
[3, 1, 2], [3, 2, 1]]
It is also possible to take the union of more than two disjoint sets, or even an infinite number of them. We will now construct the set of all permutations, viewed as the union of the sets \(P_n\) of permutations of size \(n\). We begin by constructing the infinite family \(F=(P_n)_{n\in N}\):
sage: F = Family(NonNegativeIntegers(), Permutations); F
Lazy family (<class 'sage.combinat.permutation.Permutations'>(i))_{i in Non negative integers}
sage: F.keys()
Non negative integers
sage: F[1000]
Standard permutations of 1000
>>> from sage.all import *
>>> F = Family(NonNegativeIntegers(), Permutations); F
Lazy family (<class 'sage.combinat.permutation.Permutations'>(i))_{i in Non negative integers}
>>> F.keys()
Non negative integers
>>> F[Integer(1000)]
Standard permutations of 1000
Now we can construct the disjoint union \(\bigcup_{n\in \NN}P_n\):
sage: U = DisjointUnionEnumeratedSets(F); U
Disjoint union of
Lazy family (<class 'sage.combinat.permutation.Permutations'>(i))_{i in Non negative integers}
>>> from sage.all import *
>>> U = DisjointUnionEnumeratedSets(F); U
Disjoint union of
Lazy family (<class 'sage.combinat.permutation.Permutations'>(i))_{i in Non negative integers}
It is an infinite set:
sage: U.cardinality()
+Infinity
>>> from sage.all import *
>>> U.cardinality()
+Infinity
which doesn’t prohibit iteration through its elements, though it will be necessary to interrupt it at some point:
sage: for p in U: # not tested
....: print(p)
[]
[1]
[1, 2]
[2, 1]
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
...
>>> from sage.all import *
>>> for p in U: # not tested
... print(p)
[]
[1]
[1, 2]
[2, 1]
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
...
Note: the above set could also have been constructed directly with:
sage: U = Permutations(); U
Standard permutations
>>> from sage.all import *
>>> U = Permutations(); U
Standard permutations
Summary¶
Sage provides a library of common enumerated sets, which can be
combined by standard constructions, giving a toolbox that is flexible
(but which could still be expanded). It is also possible to add new
building blocks to Sage with a few lines (see the code in
FiniteEnumeratedSets().example()). This is made possible by the
uniformity of the interfaces and the fact that Sage is based on an
object-oriented language. Also, very large or even infinite sets can
be manipulated thanks to lazy evaluation strategies (iterators, etc.).
There is no magic to any of this: under the hood, Sage applies the
usual rules (for example, that the cardinality of \(E\times E\) is
\(|E|^2\)); the added value comes from the capacity to manipulate
complicated constructions. The situation is comparable to Sage’s
implementation of differential calculus: Sage applies the usual
rules for differentiation of functions and their compositions, where
the added value comes from the possibility of manipulating complicated
formulas. In this sense, Sage implements a calculus of finite
enumerated sets.
Generic algorithms¶
Lexicographic generation of lists of integers¶
Among the classic enumerated sets, especially in algebraic combinatorics, a certain number are composed of lists of integers of fixed sum, such as partitions, compositions, or integer vectors. These examples can also have supplementary constraints added to them. Here are some examples. We start with the integer vectors with sum \(10\) and length \(3\), with parts bounded below by \(2\), \(4\) and \(2\) respectively:
sage: IntegerVectors(10, 3, min_part=2, max_part=5,
....: inner=[2, 4, 2]).list()
[[4, 4, 2], [3, 5, 2], [3, 4, 3], [2, 5, 3], [2, 4, 4]]
>>> from sage.all import *
>>> IntegerVectors(Integer(10), Integer(3), min_part=Integer(2), max_part=Integer(5),
... inner=[Integer(2), Integer(4), Integer(2)]).list()
[[4, 4, 2], [3, 5, 2], [3, 4, 3], [2, 5, 3], [2, 4, 4]]
The compositions of \(5\) with each part at most \(3\), and with length \(2\) or \(3\):
sage: Compositions(5, max_part=3,
....: min_length=2, max_length=3).list()
[[3, 2], [3, 1, 1], [2, 3], [2, 2, 1], [2, 1, 2], [1, 3, 1],
[1, 2, 2], [1, 1, 3]]
>>> from sage.all import *
>>> Compositions(Integer(5), max_part=Integer(3),
... min_length=Integer(2), max_length=Integer(3)).list()
[[3, 2], [3, 1, 1], [2, 3], [2, 2, 1], [2, 1, 2], [1, 3, 1],
[1, 2, 2], [1, 1, 3]]
The strictly decreasing partitions of \(5\):
sage: Partitions(5, max_slope=-1).list()
[[5], [4, 1], [3, 2]]
>>> from sage.all import *
>>> Partitions(Integer(5), max_slope=-Integer(1)).list()
[[5], [4, 1], [3, 2]]
These sets share the same underlying algorithmic structure, implemented
in the more general (and slightly more cumbersome) class
IntegerListsLex. This class models sets of vectors
\((\ell_0,\dots,\ell_k)\) of nonnegative integers, with
constraints on the sum and the length, and bounds on the parts and on
the consecutive differences between the parts. Here are some more
examples:
sage: IntegerListsLex(10, length=3,
....: min_part=2, max_part=5,
....: floor=[2, 4, 2]).list()
[[4, 4, 2], [3, 5, 2], [3, 4, 3], [2, 5, 3], [2, 4, 4]]
sage: IntegerListsLex(5, min_part=1, max_part=3,
....: min_length=2, max_length=3).list()
[[3, 2], [3, 1, 1], [2, 3], [2, 2, 1], [2, 1, 2],
[1, 3, 1], [1, 2, 2], [1, 1, 3]]
sage: IntegerListsLex(5, min_part=1, max_slope=-1).list()
[[5], [4, 1], [3, 2]]
sage: list(Compositions(5, max_length=2))
[[5], [4, 1], [3, 2], [2, 3], [1, 4]]
sage: list(IntegerListsLex(5, max_length=2, min_part=1))
[[5], [4, 1], [3, 2], [2, 3], [1, 4]]
>>> from sage.all import *
>>> IntegerListsLex(Integer(10), length=Integer(3),
... min_part=Integer(2), max_part=Integer(5),
... floor=[Integer(2), Integer(4), Integer(2)]).list()
[[4, 4, 2], [3, 5, 2], [3, 4, 3], [2, 5, 3], [2, 4, 4]]
>>> IntegerListsLex(Integer(5), min_part=Integer(1), max_part=Integer(3),
... min_length=Integer(2), max_length=Integer(3)).list()
[[3, 2], [3, 1, 1], [2, 3], [2, 2, 1], [2, 1, 2],
[1, 3, 1], [1, 2, 2], [1, 1, 3]]
>>> IntegerListsLex(Integer(5), min_part=Integer(1), max_slope=-Integer(1)).list()
[[5], [4, 1], [3, 2]]
>>> list(Compositions(Integer(5), max_length=Integer(2)))
[[5], [4, 1], [3, 2], [2, 3], [1, 4]]
>>> list(IntegerListsLex(Integer(5), max_length=Integer(2), min_part=Integer(1)))
[[5], [4, 1], [3, 2], [2, 3], [1, 4]]
The point of the model of IntegerListsLex is in the compromise
between generality and efficiency. The main algorithm permits
iteration through the elements of such a set \(S\) in reverse
lexicographic order with a good complexity in most practical use
cases. Roughly speaking, the time needed to iterate through all the
elements of \(S\) is proportional to the number of elements, where the
proportion factor is controlled by the length \(l\) of the longest
element of \(S\). In addition, the memory usage is also controlled by
\(l\), which is to say negligible in practice.
This algorithm is based on a very general principle for traversing a decision tree, called branch and bound: at the top level, we run through all the possible choices for \(\ell_0\); for each of these choices, we run through all the possible choices for \(\ell_1\), and so on. Mathematically speaking, we have put the structure of a prefix tree on the elements of \(S\): a node of the tree at depth \(k\) corresponds to a prefix \(\ell_0,\dots,\ell_k\) of one (or more) elements of \(S\) (see Figure: The prefix tree of the partitions of 5.).

Figure: The prefix tree of the partitions of 5.¶
The usual problem with this type of approach is to avoid bad decisions which lead to leaving the prefix tree and exploring dead branches; this is particularly problematic because the growth of the number of elements is usually exponential in the depth. It turns out that the constraints listed above are simple enough to be able to reasonably predict when a sequence \(\ell_0,\dots,\ell_k\) is a prefix of some element \(S\). Hence, most dead branches can be pruned.
Integer points in polytopes¶
Although the algorithm for iteration in IntegerListsLex is
efficient, its counting algorithm is naive: it just iterates over all
the elements.
There is an alternative approach to treating this problem: modelling the
desired lists of integers as the set of integer points of a polytope,
that is to say, the set of solutions with integer coordinates of a
system of linear inequalities. This is a very general context in which
there exist advanced counting algorithms (e.g. Barvinok), which are
implemented in libraries like LattE. Iteration does not pose a hard problem
in principle. However, there are two limitations that justify the
existence of IntegerListsLex. The first is theoretical: lattice
points in a polytope only allow modelling of problems of a fixed
dimension (length). The second is practical: at the moment only the
library PALP has a Sage interface, and though it offers multiple
capabilities for the study of polytopes, in the present application it
only produces a list of lattice points, without providing either an
iterator or non-naive counting:
sage: A = random_matrix(ZZ, 6, 3, x=7)
sage: L = LatticePolytope(A.rows())
sage: L.points() # random
M(4, 1, 0),
M(0, 3, 5),
M(2, 2, 3),
M(6, 1, 3),
M(1, 3, 6),
M(6, 2, 3),
M(3, 2, 4),
M(3, 2, 3),
M(4, 2, 4),
M(4, 2, 3),
M(5, 2, 3)
in 3-d lattice M
sage: L.npoints() # random
11
>>> from sage.all import *
>>> A = random_matrix(ZZ, Integer(6), Integer(3), x=Integer(7))
>>> L = LatticePolytope(A.rows())
>>> L.points() # random
M(4, 1, 0),
M(0, 3, 5),
M(2, 2, 3),
M(6, 1, 3),
M(1, 3, 6),
M(6, 2, 3),
M(3, 2, 4),
M(3, 2, 3),
M(4, 2, 4),
M(4, 2, 3),
M(5, 2, 3)
in 3-d lattice M
>>> L.npoints() # random
11
This polytope can be visualized in 3D with L.plot3d() (see
Figure: The polytope L and its integer points, in cross-eyed stereographic perspective.).
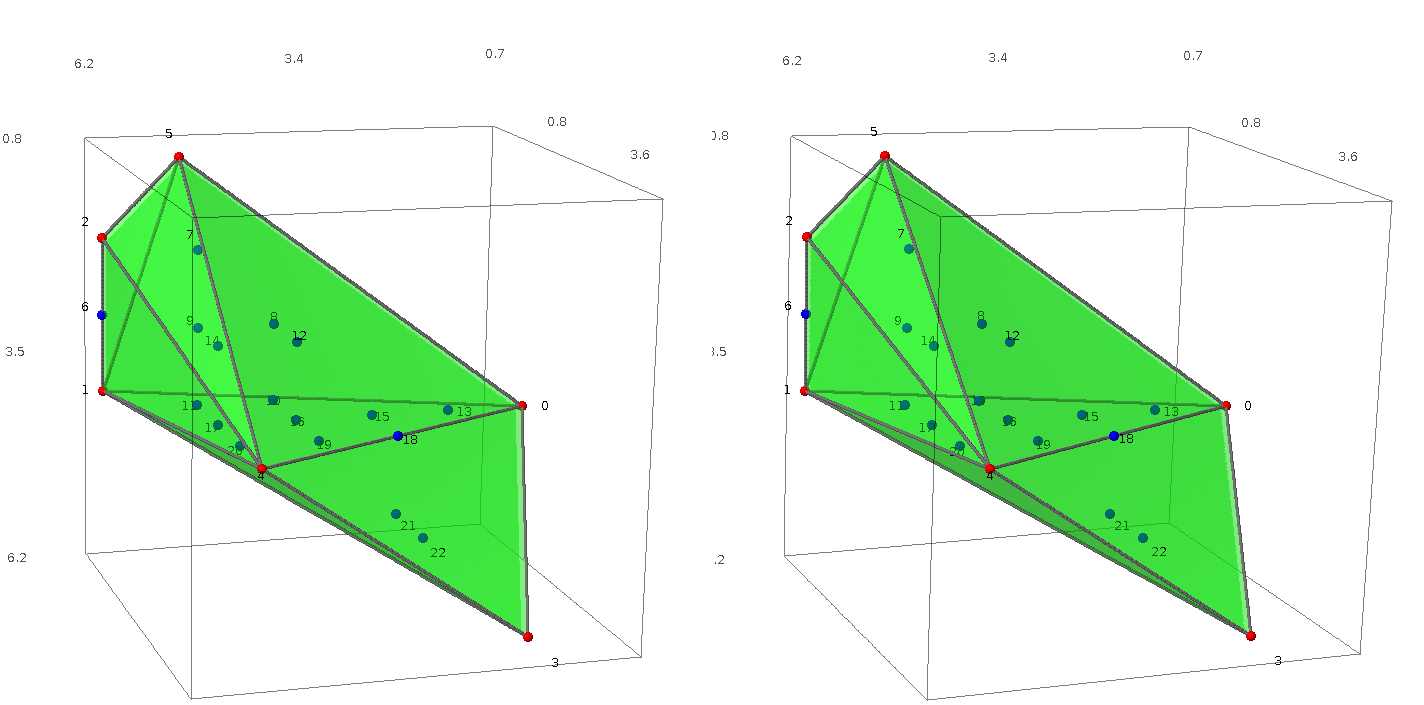
Figure: The polytope \(L\) and its integer points, in cross-eyed stereographic perspective.¶
Species, decomposable combinatorial classes¶
In Enumeration of trees using generating functions, we showed how to use the recursive definition of binary trees to count them efficiently using generating functions. The techniques we used there are very general, and apply whenever the sets involved can be defined recursively (depending on who you ask, such a set is called a decomposable combinatorial class or, roughly speaking, a combinatorial species). This includes all the types of trees, but also permutations, compositions, functional graphs, etc.
Here, we illustrate just a few examples using the Sage library on
combinatorial species:
sage: from sage.combinat.species.library import *
sage: o = var('o') # needs sage.symbolic
>>> from sage.all import *
>>> from sage.combinat.species.library import *
>>> o = var('o') # needs sage.symbolic
We begin by redefining the complete binary trees; to do so, we stipulate the recurrence relation directly on the sets:
sage: BT = CombinatorialSpecies(min=1)
sage: Leaf = SingletonSpecies()
sage: BT.define( Leaf + (BT*BT) )
>>> from sage.all import *
>>> BT = CombinatorialSpecies(min=Integer(1))
>>> Leaf = SingletonSpecies()
>>> BT.define( Leaf + (BT*BT) )
Now we can construct the set of trees with five nodes, list them, count them…:
sage: BT5 = BT.isotypes([o]*5) # needs sage.symbolic
sage: BT5.cardinality() # needs sage.symbolic
14
sage: BT5.list() # needs sage.symbolic
[o*(o*(o*(o*o))), o*(o*((o*o)*o)), o*((o*o)*(o*o)),
o*((o*(o*o))*o), o*(((o*o)*o)*o), (o*o)*(o*(o*o)),
(o*o)*((o*o)*o), (o*(o*o))*(o*o), ((o*o)*o)*(o*o),
(o*(o*(o*o)))*o, (o*((o*o)*o))*o, ((o*o)*(o*o))*o,
((o*(o*o))*o)*o, (((o*o)*o)*o)*o]
>>> from sage.all import *
>>> BT5 = BT.isotypes([o]*Integer(5)) # needs sage.symbolic
>>> BT5.cardinality() # needs sage.symbolic
14
>>> BT5.list() # needs sage.symbolic
[o*(o*(o*(o*o))), o*(o*((o*o)*o)), o*((o*o)*(o*o)),
o*((o*(o*o))*o), o*(((o*o)*o)*o), (o*o)*(o*(o*o)),
(o*o)*((o*o)*o), (o*(o*o))*(o*o), ((o*o)*o)*(o*o),
(o*(o*(o*o)))*o, (o*((o*o)*o))*o, ((o*o)*(o*o))*o,
((o*(o*o))*o)*o, (((o*o)*o)*o)*o]
The trees are constructed using a generic recursive structure; the
display is therefore not wonderful. To do better, it would be necessary
to provide Sage with a more specialized data structure with the
desired display capabilities.
We recover the generating function for the Catalan numbers:
sage: g = BT.isotype_generating_series(); g
z + z^2 + 2*z^3 + 5*z^4 + 14*z^5 + 42*z^6 + 132*z^7 + O(z^8)
>>> from sage.all import *
>>> g = BT.isotype_generating_series(); g
z + z^2 + 2*z^3 + 5*z^4 + 14*z^5 + 42*z^6 + 132*z^7 + O(z^8)
which is returned in the form of a lazy power series:
sage: g[100]
227508830794229349661819540395688853956041682601541047340
>>> from sage.all import *
>>> g[Integer(100)]
227508830794229349661819540395688853956041682601541047340
We finish with the Fibonacci words, which are binary words without two consecutive “\(1\)”s. They admit a natural recursive definition:
sage: Eps = EmptySetSpecies()
sage: Z0 = SingletonSpecies()
sage: Z1 = Eps*SingletonSpecies()
sage: FW = CombinatorialSpecies()
sage: FW.define(Eps + Z0*FW + Z1*Eps + Z1*Z0*FW)
>>> from sage.all import *
>>> Eps = EmptySetSpecies()
>>> Z0 = SingletonSpecies()
>>> Z1 = Eps*SingletonSpecies()
>>> FW = CombinatorialSpecies()
>>> FW.define(Eps + Z0*FW + Z1*Eps + Z1*Z0*FW)
The Fibonacci sequence is easily recognized here, hence the name:
sage: L = FW.isotype_generating_series()[:15]; L
[1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987]
>>> from sage.all import *
>>> L = FW.isotype_generating_series()[:Integer(15)]; L
[1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987]
sage: oeis(L) # optional -- internet
0: A000045: Fibonacci numbers: F(n) = F(n-1) + F(n-2) with F(0) = 0 and F(1) = 1.
1: ...
2: ...
>>> from sage.all import *
>>> oeis(L) # optional -- internet
0: A000045: Fibonacci numbers: F(n) = F(n-1) + F(n-2) with F(0) = 0 and F(1) = 1.
1: ...
2: ...
This is an immediate consequence of the recurrence relation. One can also generate immediately all the Fibonacci words of a given length, with the same limitations resulting from the generic display.
sage: FW3 = FW.isotypes([o]*3) # needs sage.symbolic
sage: FW3.list() # needs sage.symbolic
[o*(o*(o*{})), o*(o*(({}*o)*{})), o*((({}*o)*o)*{}),
(({}*o)*o)*(o*{}), (({}*o)*o)*(({}*o)*{})]
>>> from sage.all import *
>>> FW3 = FW.isotypes([o]*Integer(3)) # needs sage.symbolic
>>> FW3.list() # needs sage.symbolic
[o*(o*(o*{})), o*(o*(({}*o)*{})), o*((({}*o)*o)*{}),
(({}*o)*o)*(o*{}), (({}*o)*o)*(({}*o)*{})]
Graphs up to isomorphism¶
We saw in Some other finite enumerated sets that Sage could generate
graphs and partial orders up to isomorphism. We will now describe the
underlying algorithm, which is the same in both cases, and covers a
substantially wider class of problems.
We begin by recalling some notions. A graph \(G=(V,E)\) is a set \(V\) of vertices and a set \(E\) of edges connecting these vertices; an edge is described by a pair \(\{u,v\}\) of distinct vertices of \(V\). Such a graph is called labelled; its vertices are typically numbered by considering \(V=\{1,2,3,4,5\}\).
In many problems, the labels on the vertices play no role. Typically a chemist wants to study all the possible molecules with a given composition, for example the alkanes with \(n=8\) atoms of carbon and \(2n+2=18\) atoms of hydrogen. He therefore wants to find all the graphs consisting of \(8\) vertices with \(4\) neighbours, and \(18\) vertices with a single neighbour. The different carbon atoms, however, are all considered to be identical, and the same for the hydrogen atoms. The problem of our chemist is not imaginary; this type of application is actually at the origin of an important part of the research in graph theory on isomorphism problems.
Working by hand on a small graph it is possible, as in the example of Some other finite enumerated sets, to make a drawing, erase the labels, and “forget” the geometrical information about the location of the vertices in the plane. However, to represent a graph in a computer program, it is necessary to introduce labels on the vertices so as to be able to describe how the edges connect them together. To compensate for the extra information which we have introduced, we then say that two labelled graphs \(g_1\) and \(g_2\) are isomorphic if there is a bijection from the vertices of \(g_1\) to those of \(g_2\), which maps bijectively the edges of \(g_1\) to those of \(g_2\); an unlabelled graph is then an equivalence class of labelled graphs.
In general, testing if two labelled graphs are isomorphic is expensive.
However, the number of graphs, even unlabelled, grows very
rapidly. Nonetheless, it is possible to list unlabelled graphs very efficiently
considering their number. For example, the program Nauty can list the
\(12005168\) simple graphs with \(10\) vertices in
\(20\) seconds.
As in Lexicographic generation of lists of integers, the general principle of the algorithm is to organize the objects to be enumerated into a tree that one traverses.
For this, in each equivalence class of labelled graphs (that is to say, for each unlabelled graph) one fixes a convenient canonical representative. The following are the fundamental operations:
Testing whether a labelled graph is canonical
Calculating the canonical representative of a labelled graph
These unavoidable operations remain expensive; one therefore tries to minimize the number of calls to them.
The canonical representatives are chosen in such a way that, for each canonical labelled graph \(G\), there is a canonical choice of an edge whose removal produces a canonical graph again, which is called the father of \(G\). This property implies that it is possible to organize the set of canonical representatives as a tree: at the root, the graph with no edges; below it, its unique child, the graph with one edge; then the graphs with two edges, and so on. The set of children of a graph \(G\) can be constructed by augmentation, adding an edge in all the possible ways to \(G\), and then selecting, from among those graphs, the ones that are still canonical [2]. Recursively, one obtains all the canonical graphs.

Figure: The generation tree of simple graphs with \(4\) vertices.¶
In what sense is this algorithm generic? Consider for example planar graphs (graphs which can be drawn in the plane without edges crossing): by removing an edge from a planar graph, one obtains another planar graph; so planar graphs form a subtree of the previous tree. To generate them, exactly the same algorithm can be used, selecting only the children which are planar:
sage: [len(list(graphs(n, property=lambda G: G.is_planar())))
....: for n in range(7)]
[1, 1, 2, 4, 11, 33, 142]
>>> from sage.all import *
>>> [len(list(graphs(n, property=lambda G: G.is_planar())))
... for n in range(Integer(7))]
[1, 1, 2, 4, 11, 33, 142]
In a similar fashion, one can generate any family of graphs closed under deletion of an edge, and in particular any family characterized by a forbidden subgraph. This includes for example forests (graphs without cycles), bipartite graphs (graphs without odd cycles), etc. This can be applied to generate:
partial orders, via the bijection with Hasse diagrams which are oriented graphs without cycles and without edges implied by the transitivity of the order relation;
lattices (not implemented in
Sage), via the bijection with the meet semi-lattice obtained by deleting the maximal vertex; in this case an augmentation by vertices rather than by edges is used.
REFERENCES:
[CMS2012]Alexandre Casamayou, Nathann Cohen, Guillaume Connan, Thierry Dumont, Laurent Fousse, François Maltey, Matthias Meulien, Marc Mezzarobba, Clément Pernet, Nicolas M. Thiéry, Paul Zimmermann Calcul Mathématique avec Sage https://www.sagemath.org/sagebook/french.html