Sage Quickstart for Graph Theory and Discrete Mathematics¶
This Sage quickstart tutorial was developed for the MAA PREP Workshop “Sage: Using Open-Source Mathematics Software with Undergraduates” (funding provided by NSF DUE 0817071). It is licensed under the Creative Commons Attribution-ShareAlike 3.0 license (CC BY-SA).
As computers are discrete and finite, topics from discrete mathematics are natural to implement and use. We’ll start with Graph Theory.
Graph Theory¶
The pre-defined graphs object provides an abundance of examples.
Just tab to see!
sage: graphs.[tab]
>>> from sage.all import *
>>> graphs.[tab]
Its companion digraphs has many built-in examples as well.
Visualizing a graph is similar to plotting functions.
sage: G = graphs.HeawoodGraph()
sage: plot(G)
Graphics object consisting of 36 graphics primitives
>>> from sage.all import *
>>> G = graphs.HeawoodGraph()
>>> plot(G)
Graphics object consisting of 36 graphics primitives
Defining your own graph is easy. One way is the following.
Put a vertex next to a list (recall this concept from the programming tutorial) with a colon, to show its adjacent vertices. For example, to put vertex 4 next to vertices 0 and 2, use
4:[0,2].Now combine all these in curly braces (in the advanced appendix to the programming tutorial, this is called a dictionary ).
sage: H=Graph({0:[1,2,3], 4:[0,2], 6:[1,2,3,4,5]})
sage: plot(H)
Graphics object consisting of 18 graphics primitives
>>> from sage.all import *
>>> H=Graph({Integer(0):[Integer(1),Integer(2),Integer(3)], Integer(4):[Integer(0),Integer(2)], Integer(6):[Integer(1),Integer(2),Integer(3),Integer(4),Integer(5)]})
>>> plot(H)
Graphics object consisting of 18 graphics primitives
Adjacency matrices, other graphs, and similar inputs are also recognized.
Graphs have “position” information for location of vertices. There are several different ways to compute a layout, or you can compute your own. Pre-defined graphs often come with “nice” layouts.
sage: H.set_pos(H.layout_circular())
sage: plot(H)
Graphics object consisting of 18 graphics primitives
>>> from sage.all import *
>>> H.set_pos(H.layout_circular())
>>> plot(H)
Graphics object consisting of 18 graphics primitives
Vertices can be lots of things, for example the codewords of an error-correcting code.
Note
Technical caveat: they need to be “immutable”, like Python’s tuples.
Here we have a matrix over the integers and a matrix of variables as vertices.
sage: a=matrix([[1,2],[3,4]])
sage: var('x y z w')
(x, y, z, w)
sage: b=matrix([[x,y],[z,w]])
sage: a.set_immutable()
sage: b.set_immutable()
sage: K=DiGraph({a:[b]})
sage: show(K, vertex_size=800)
>>> from sage.all import *
>>> a=matrix([[Integer(1),Integer(2)],[Integer(3),Integer(4)]])
>>> var('x y z w')
(x, y, z, w)
>>> b=matrix([[x,y],[z,w]])
>>> a.set_immutable()
>>> b.set_immutable()
>>> K=DiGraph({a:[b]})
>>> show(K, vertex_size=Integer(800))
Edges can be labeled.
sage: L=graphs.CycleGraph(5)
sage: for edge in L.edges(sort=True):
....: u = edge[0]
....: v = edge[1]
....: L.set_edge_label(u, v, u*v)
sage: plot(L, edge_labels=True)
Graphics object consisting of 16 graphics primitives
>>> from sage.all import *
>>> L=graphs.CycleGraph(Integer(5))
>>> for edge in L.edges(sort=True):
... u = edge[Integer(0)]
... v = edge[Integer(1)]
... L.set_edge_label(u, v, u*v)
>>> plot(L, edge_labels=True)
Graphics object consisting of 16 graphics primitives
There are natural connections to other areas of mathematics. Here we compute the automorphism group and eigenvalues of the skeleton of a cube.
sage: C = graphs.CubeGraph(3)
sage: plot(C)
Graphics object consisting of 21 graphics primitives
>>> from sage.all import *
>>> C = graphs.CubeGraph(Integer(3))
>>> plot(C)
Graphics object consisting of 21 graphics primitives
sage: Aut=C.automorphism_group()
sage: print("Order of automorphism group: {}".format(Aut.order()))
Order of automorphism group: 48
sage: print("Group: \n{}".format(Aut)) # random
Group:
Permutation Group with generators [('010','100')('011','101'), ('001','010')('101','110'), ('000','001')('010','011')('100','101')('110','111')]
>>> from sage.all import *
>>> Aut=C.automorphism_group()
>>> print("Order of automorphism group: {}".format(Aut.order()))
Order of automorphism group: 48
>>> print("Group: \n{}".format(Aut)) # random
Group:
Permutation Group with generators [('010','100')('011','101'), ('001','010')('101','110'), ('000','001')('010','011')('100','101')('110','111')]
sage: C.spectrum()
[3, 1, 1, 1, -1, -1, -1, -3]
>>> from sage.all import *
>>> C.spectrum()
[3, 1, 1, 1, -1, -1, -1, -3]
There is a huge amount of LaTeX support for graphs. The following graphic shows an example of what can be done; this is the Heawood graph.
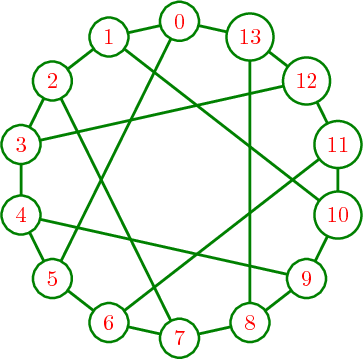
Press ‘tab’ at the next command to see all the available options.
sage: sage.graphs.graph_latex.GraphLatex.set_option?
>>> from sage.all import *
>>> sage.graphs.graph_latex.GraphLatex.set_option?
More Discrete Mathematics¶
Discrete mathematics is a broad area, and Sage has excellent support for much of it. This is largely due to the “sage-combinat” group. These developers previously developed for MuPad (as “mupad-combinat”) but switched over to Sage shortly before MuPad was sold.
Simple Combinatorics¶
Sage can work with basic combinatorial structures like combinations and permutations.
sage: pets = ['dog', 'cat', 'snake', 'spider']
sage: C=Combinations(pets)
sage: C.list()
[[], ['dog'], ['cat'], ['snake'], ['spider'], ['dog', 'cat'], ['dog', 'snake'], ['dog', 'spider'], ['cat', 'snake'], ['cat', 'spider'], ['snake', 'spider'], ['dog', 'cat', 'snake'], ['dog', 'cat', 'spider'], ['dog', 'snake', 'spider'], ['cat', 'snake', 'spider'], ['dog', 'cat', 'snake', 'spider']]
>>> from sage.all import *
>>> pets = ['dog', 'cat', 'snake', 'spider']
>>> C=Combinations(pets)
>>> C.list()
[[], ['dog'], ['cat'], ['snake'], ['spider'], ['dog', 'cat'], ['dog', 'snake'], ['dog', 'spider'], ['cat', 'snake'], ['cat', 'spider'], ['snake', 'spider'], ['dog', 'cat', 'snake'], ['dog', 'cat', 'spider'], ['dog', 'snake', 'spider'], ['cat', 'snake', 'spider'], ['dog', 'cat', 'snake', 'spider']]
sage: for a, b in Combinations(pets, 2):
....: print("The {} chases the {}.".format(a, b))
The dog chases the cat.
The dog chases the snake.
The dog chases the spider.
The cat chases the snake.
The cat chases the spider.
The snake chases the spider.
>>> from sage.all import *
>>> for a, b in Combinations(pets, Integer(2)):
... print("The {} chases the {}.".format(a, b))
The dog chases the cat.
The dog chases the snake.
The dog chases the spider.
The cat chases the snake.
The cat chases the spider.
The snake chases the spider.
sage: for pair in Permutations(pets, 2):
....: print(pair)
['dog', 'cat']
['dog', 'snake']
['dog', 'spider']
['cat', 'dog']
['cat', 'snake']
['cat', 'spider']
['snake', 'dog']
['snake', 'cat']
['snake', 'spider']
['spider', 'dog']
['spider', 'cat']
['spider', 'snake']
>>> from sage.all import *
>>> for pair in Permutations(pets, Integer(2)):
... print(pair)
['dog', 'cat']
['dog', 'snake']
['dog', 'spider']
['cat', 'dog']
['cat', 'snake']
['cat', 'spider']
['snake', 'dog']
['snake', 'cat']
['snake', 'spider']
['spider', 'dog']
['spider', 'cat']
['spider', 'snake']
Of course, we often want these for numbers, and these are present as well. Some are familiar:
sage: Permutations(5).cardinality()
120
>>> from sage.all import *
>>> Permutations(Integer(5)).cardinality()
120
Others somewhat less so:
sage: D = Derangements([1,1,2,2,3,4,5])
sage: D.list()[:5]
[[2, 2, 1, 1, 4, 5, 3], [2, 2, 1, 1, 5, 3, 4], [2, 2, 1, 3, 1, 5, 4], [2, 2, 1, 3, 4, 5, 1], [2, 2, 1, 3, 5, 1, 4]]
>>> from sage.all import *
>>> D = Derangements([Integer(1),Integer(1),Integer(2),Integer(2),Integer(3),Integer(4),Integer(5)])
>>> D.list()[:Integer(5)]
[[2, 2, 1, 1, 4, 5, 3], [2, 2, 1, 1, 5, 3, 4], [2, 2, 1, 3, 1, 5, 4], [2, 2, 1, 3, 4, 5, 1], [2, 2, 1, 3, 5, 1, 4]]
And some somewhat more advanced – in this case, symmetric polynomials.
sage: s = SymmetricFunctions(QQ).schur()
sage: a = s([2,1])
sage: a.expand(3)
x0^2*x1 + x0*x1^2 + x0^2*x2 + 2*x0*x1*x2 + x1^2*x2 + x0*x2^2 + x1*x2^2
>>> from sage.all import *
>>> s = SymmetricFunctions(QQ).schur()
>>> a = s([Integer(2),Integer(1)])
>>> a.expand(Integer(3))
x0^2*x1 + x0*x1^2 + x0^2*x2 + 2*x0*x1*x2 + x1^2*x2 + x0*x2^2 + x1*x2^2
Various functions related to this are available as well.
sage: binomial(25,3)
2300
>>> from sage.all import *
>>> binomial(Integer(25),Integer(3))
2300
sage: multinomial(24,3,5)
589024800
>>> from sage.all import *
>>> multinomial(Integer(24),Integer(3),Integer(5))
589024800
sage: falling_factorial(10,4)
5040
>>> from sage.all import *
>>> falling_factorial(Integer(10),Integer(4))
5040
Do you recognize this famous identity?
sage: var('k,n')
(k, n)
sage: sum(binomial(n,k),k,0,n)
2^n
>>> from sage.all import *
>>> var('k,n')
(k, n)
>>> sum(binomial(n,k),k,Integer(0),n)
2^n
Cryptography (for education)¶
This is also briefly mentioned in the Number theory quickstart. Sage has a number of good pedagogical resources for cryptography.
sage: # Two objects to make/use encryption scheme
sage: #
sage: from sage.crypto.block_cipher.sdes import SimplifiedDES
sage: sdes = SimplifiedDES()
sage: bin = BinaryStrings()
sage: #
sage: # Convert English to binary
sage: #
sage: P = bin.encoding("Encrypt this using S-DES!")
sage: print("Binary plaintext: {}\n".format(P))
sage: #
sage: # Choose a random key
sage: #
sage: K = sdes.list_to_string(sdes.random_key())
sage: print("Random key: {}\n".format(K))
sage: #
sage: # Encrypt with Simplified DES
sage: #
sage: C = sdes(P, K, algorithm="encrypt")
sage: print("Encrypted: {}\n".format(C))
sage: #
sage: # Decrypt for the round-trip
sage: #
sage: plaintxt = sdes(C, K, algorithm="decrypt")
sage: print("Decrypted: {}\n".format(plaintxt))
sage: #
sage: # Verify easily
sage: #
sage: print("Verify encryption/decryption: {}".format(P == plaintxt))
Binary plaintext: 01000101011011100110001101110010011110010111000001110100001000000111010001101000011010010111001100100000011101010111001101101001011011100110011100100000010100110010110101000100010001010101001100100001
Random key: 0100000011
Encrypted: 00100001100001010011000111000110010000011011101011111011100011011111101111110111110010101000010010001101101010101000010011001010100001010111000010001101000011001001111111110100001000010000110001011000
Decrypted: 01000101011011100110001101110010011110010111000001110100001000000111010001101000011010010111001100100000011101010111001101101001011011100110011100100000010100110010110101000100010001010101001100100001
Verify encryption/decryption: True
>>> from sage.all import *
>>> # Two objects to make/use encryption scheme
>>> #
>>> from sage.crypto.block_cipher.sdes import SimplifiedDES
>>> sdes = SimplifiedDES()
>>> bin = BinaryStrings()
>>> #
>>> # Convert English to binary
>>> #
>>> P = bin.encoding("Encrypt this using S-DES!")
>>> print("Binary plaintext: {}\n".format(P))
>>> #
>>> # Choose a random key
>>> #
>>> K = sdes.list_to_string(sdes.random_key())
>>> print("Random key: {}\n".format(K))
>>> #
>>> # Encrypt with Simplified DES
>>> #
>>> C = sdes(P, K, algorithm="encrypt")
>>> print("Encrypted: {}\n".format(C))
>>> #
>>> # Decrypt for the round-trip
>>> #
>>> plaintxt = sdes(C, K, algorithm="decrypt")
>>> print("Decrypted: {}\n".format(plaintxt))
>>> #
>>> # Verify easily
>>> #
>>> print("Verify encryption/decryption: {}".format(P == plaintxt))
Binary plaintext: 01000101011011100110001101110010011110010111000001110100001000000111010001101000011010010111001100100000011101010111001101101001011011100110011100100000010100110010110101000100010001010101001100100001
Random key: 0100000011
Encrypted: 00100001100001010011000111000110010000011011101011111011100011011111101111110111110010101000010010001101101010101000010011001010100001010111000010001101000011001001111111110100001000010000110001011000
Decrypted: 01000101011011100110001101110010011110010111000001110100001000000111010001101000011010010111001100100000011101010111001101101001011011100110011100100000010100110010110101000100010001010101001100100001
Verify encryption/decryption: True
Coding Theory¶
Here is a brief example of a linear binary code (group code).
Start with a generator matrix over \(\ZZ/2\ZZ\).
sage: G = matrix(GF(2), [[1,1,1,0,0,0,0], [1,0,0,1,1,0,0], [0,1,0,1,0,1,0], [1,1,0,1,0,0,1]])
sage: C = LinearCode(G)
>>> from sage.all import *
>>> G = matrix(GF(Integer(2)), [[Integer(1),Integer(1),Integer(1),Integer(0),Integer(0),Integer(0),Integer(0)], [Integer(1),Integer(0),Integer(0),Integer(1),Integer(1),Integer(0),Integer(0)], [Integer(0),Integer(1),Integer(0),Integer(1),Integer(0),Integer(1),Integer(0)], [Integer(1),Integer(1),Integer(0),Integer(1),Integer(0),Integer(0),Integer(1)]])
>>> C = LinearCode(G)
sage: C.is_self_dual()
False
>>> from sage.all import *
>>> C.is_self_dual()
False
sage: D = C.dual_code()
sage: D
[7, 3] linear code over GF(2)
>>> from sage.all import *
>>> D = C.dual_code()
>>> D
[7, 3] linear code over GF(2)
sage: D.basis()
[(1, 0, 1, 0, 1, 0, 1), (0, 1, 1, 0, 0, 1, 1), (0, 0, 0, 1, 1, 1, 1)]
>>> from sage.all import *
>>> D.basis()
[(1, 0, 1, 0, 1, 0, 1), (0, 1, 1, 0, 0, 1, 1), (0, 0, 0, 1, 1, 1, 1)]
sage: D.permutation_automorphism_group()
Permutation Group with generators [(4,5)(6,7), (4,6)(5,7), (2,3)(6,7), (2,4)(3,5), (1,2)(5,6)]
>>> from sage.all import *
>>> D.permutation_automorphism_group()
Permutation Group with generators [(4,5)(6,7), (4,6)(5,7), (2,3)(6,7), (2,4)(3,5), (1,2)(5,6)]