\(n\)-Cube¶
This section provides some examples on Chapter 2 of Stanley’s book [Stanley2013], which deals with \(n\)-cubes, the Radon transform, and combinatorial formulas for walks on the \(n\)-cube.
The vertices of the \(n\)-cube can be described by vectors in \(\mathbb{Z}_2^n\). First we define the addition of two vectors \(u,v \in \mathbb{Z}_2^n\) via the following distance:
sage: def dist(u,v):
....: h = [(u[i]+v[i])%2 for i in range(len(u))]
....: return sum(h)
>>> from sage.all import *
>>> def dist(u,v):
... h = [(u[i]+v[i])%Integer(2) for i in range(len(u))]
... return sum(h)
The distance function measures in how many slots two vectors in \(\mathbb{Z}_2^n\) differ:
sage: u = (1,0,1,1,1,0)
sage: v = (0,0,1,1,0,0)
sage: dist(u,v)
2
>>> from sage.all import *
>>> u = (Integer(1),Integer(0),Integer(1),Integer(1),Integer(1),Integer(0))
>>> v = (Integer(0),Integer(0),Integer(1),Integer(1),Integer(0),Integer(0))
>>> dist(u,v)
2
Now we are going to define the \(n\)-cube as the graph with vertices in \(\mathbb{Z}_2^n\) and edges between vertex \(u\) and vertex \(v\) if they differ in one slot, that is, the distance function is 1:
sage: def cube(n):
....: G = Graph(2**n)
....: vertices = Tuples([0,1],n)
....: for i in range(2**n):
....: for j in range(2**n):
....: if dist(vertices[i],vertices[j]) == 1:
....: G.add_edge(i,j)
....: return G
>>> from sage.all import *
>>> def cube(n):
... G = Graph(Integer(2)**n)
... vertices = Tuples([Integer(0),Integer(1)],n)
... for i in range(Integer(2)**n):
... for j in range(Integer(2)**n):
... if dist(vertices[i],vertices[j]) == Integer(1):
... G.add_edge(i,j)
... return G
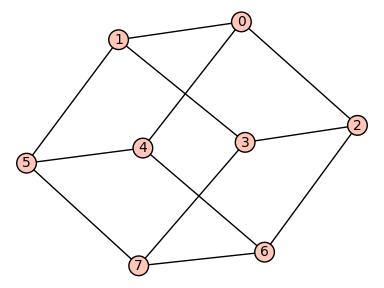
We can plot the \(3\) and \(4\)-cube:
sage: cube(3).plot()
Graphics object consisting of 21 graphics primitives
>>> from sage.all import *
>>> cube(Integer(3)).plot()
Graphics object consisting of 21 graphics primitives
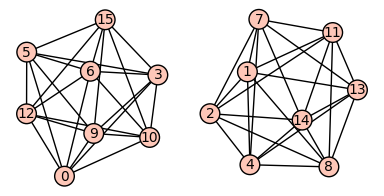
sage: cube(4).plot()
Graphics object consisting of 49 graphics primitives
>>> from sage.all import *
>>> cube(Integer(4)).plot()
Graphics object consisting of 49 graphics primitives
Next we can experiment and check Corollary 2.4 in Stanley’s book, which states the \(n\)-cube has \(n\) choose \(i\) eigenvalues equal to \(n-2i\):
sage: G = cube(2)
sage: G.adjacency_matrix().eigenvalues()
[2, -2, 0, 0]
sage: G = cube(3)
sage: G.adjacency_matrix().eigenvalues()
[3, -3, 1, 1, 1, -1, -1, -1]
sage: G = cube(4)
sage: G.adjacency_matrix().eigenvalues()
[4, -4, 2, 2, 2, 2, -2, -2, -2, -2, 0, 0, 0, 0, 0, 0]
>>> from sage.all import *
>>> G = cube(Integer(2))
>>> G.adjacency_matrix().eigenvalues()
[2, -2, 0, 0]
>>> G = cube(Integer(3))
>>> G.adjacency_matrix().eigenvalues()
[3, -3, 1, 1, 1, -1, -1, -1]
>>> G = cube(Integer(4))
>>> G.adjacency_matrix().eigenvalues()
[4, -4, 2, 2, 2, 2, -2, -2, -2, -2, 0, 0, 0, 0, 0, 0]
It is now easy to slightly vary this problem and change the edge set by connecting vertices \(u\) and \(v\) if their distance is 2 (see Problem 4 in Chapter 2):
sage: def cube_2(n):
....: G = Graph(2**n)
....: vertices = Tuples([0,1],n)
....: for i in range(2**n):
....: for j in range(2**n):
....: if dist(vertices[i],vertices[j]) == 2:
....: G.add_edge(i,j)
....: return G
sage: G = cube_2(2)
sage: G.adjacency_matrix().eigenvalues()
[1, 1, -1, -1]
sage: G = cube_2(4)
sage: G.adjacency_matrix().eigenvalues()
[6, 6, -2, -2, -2, -2, -2, -2, 0, 0, 0, 0, 0, 0, 0, 0]
>>> from sage.all import *
>>> def cube_2(n):
... G = Graph(Integer(2)**n)
... vertices = Tuples([Integer(0),Integer(1)],n)
... for i in range(Integer(2)**n):
... for j in range(Integer(2)**n):
... if dist(vertices[i],vertices[j]) == Integer(2):
... G.add_edge(i,j)
... return G
>>> G = cube_2(Integer(2))
>>> G.adjacency_matrix().eigenvalues()
[1, 1, -1, -1]
>>> G = cube_2(Integer(4))
>>> G.adjacency_matrix().eigenvalues()
[6, 6, -2, -2, -2, -2, -2, -2, 0, 0, 0, 0, 0, 0, 0, 0]
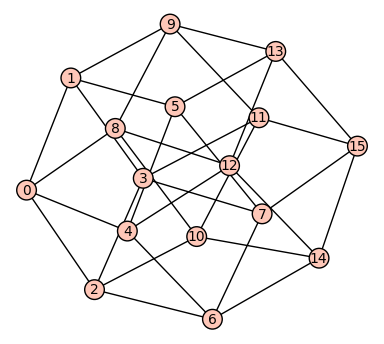
Note that the graph is in fact disconnected. Do you understand why?
sage: cube_2(4).plot()
Graphics object consisting of 65 graphics primitives
>>> from sage.all import *
>>> cube_2(Integer(4)).plot()
Graphics object consisting of 65 graphics primitives