Lie Group Basics

Goals of this section

Since we must be brief here, this is not really a place to learn about Lie groups or Lie algebras. Rather, the point of this section is to outline what you need to know to use Sage effectively for Lie computations, and to fix ideas and notations.

Semisimple and reductive groups

If \(g \in GL(n,\CC)\), then \(g\) may be uniquely factored as \(g_1 g_2\) where \(g_1\) and \(g_2\) commute, with \(g_1\) semisimple (diagonalizable) and \(g_2\) unipotent (all its eigenvalues equal to 1). This follows from the Jordan canonical form. If \(g = g_1\) then \(g\) is called semisimple and if \(g = g_2\) then \(g\) is called unipotent.

We consider a Lie group \(G\) and a class of representations such that if an element \(g \in G\) is unipotent (resp. semisimple) in one faithful representation from the class, then it is unipotent (resp. semisimple) in every faithful representation of the class. Thus the notion of being semisimple or unipotent is intrinsic. Examples:

• Compact Lie groups with continuous representations

• Complex analytic groups with analytic representations

• Algebraic groups over \(\RR\) with algebraic representations.

A subgroup of \(G\) is called unipotent if it is connected and all its elements are unipotent. It is called a torus if it is connected, abelian, and all its elements are semisimple. The group \(G\) is called reductive if it has no nontrivial normal unipotent subgroup. For example, \(GL(2,\CC)\) is reductive, but its subgroup:

\[\begin{split}\left\{\left( \begin{array}{cc} a & b \\ & d \end{array} \right)\right\}\end{split}\]

is not since it has a normal unipotent subgroup

\[\begin{split}\left\{\left( \begin{array}{cc} 1 & b \\ & 1 \end{array} \right)\right\}.\end{split}\]

A group has a unique largest normal unipotent subgroup, called the unipotent radical, so it is reductive if and only if the unipotent radical is trivial.

A Lie group is called semisimple it is reductive and furthermore has no nontrivial normal tori. For example \(GL(2,\CC)\) is reductive but not semisimple because it has a normal torus:

\[\begin{split}\left\{\left( \begin{array}{cc} a \\ & a \end{array} \right)\right\}.\end{split}\]

The group \(SL(2,\CC)\) is semisimple.

Fundamental group and center

If \(G\) is a semisimple Lie group then its center and fundamental group are finite abelian groups. The universal covering group \(\tilde G\) is therefore a finite extension with the same Lie algebra. Any representation of \(G\) may be reinterpreted as a representation of the simply connected \(\tilde G\). Therefore we may as well consider representations of \(\tilde G\), and restrict ourselves to the simply connected group.

Parabolic subgroups and Levi subgroups

Let \(G\) be a reductive complex analytic group. A maximal solvable subgroup of \(G\) is called a Borel subgroup. All Borel subgroups are conjugate. Any subgroup \(P\) containing a Borel subgroup is called a parabolic subgroup. We may write \(P\) as a semidirect product of its maximal normal unipotent subgroup or unipotent radical \(P\) and a reductive subgroup \(M\), which is determined up to conjugacy. The subgroup \(M\) is called a Levi subgroup.

Example: Let \(G = GL_n(\CC)\) and let \(r_1, \ldots, r_k\) be integers whose sum is \(n\). Then we may consider matrices of the form:

\[\begin{split}\left(\begin{array}{cccc} g_1 & * & \cdots & * \\ & g_2 & & * \\ && \ddots \\ &&& g_r \end{array}\right)\end{split}\]

where \(g_i \in GL(r_i,\CC)\). The unipotent radical consists of the subgroup in which all \(g_i = I_{r_i}\). The Levi subgroup (determined up to conjugacy) is:

\[\begin{split}M = \left\{\left( \begin{array}{cccc} g_1 \\ & g_2 \\ && \ddots \\ &&& g_r \end{array} \right)\right\},\end{split}\]

and is isomorphic to \(M = GL(r_1,\CC) \times \cdots \times GL(r_k,\CC)\). Therefore \(M\) is a Levi subgroup.

The notion of a Levi subgroup can be extended to compact Lie groups. Thus \(U(r_1) \times \cdots \times U(r_k)\) is a Levi subgroup of \(U(n)\). However parabolic subgroups do not exist for compact Lie groups.

Cartan types

Semisimple Lie groups are classified by their Cartan types. There are both reducible and irreducible Cartan types in Sage. Let us start with the irreducible types. Such a type is implemented in Sage as a pair ['X', r] where ‘X’ is one of A, B, C, D, E, F or G and \(r\) is a positive integer. If ‘X’ is ‘D’ then we must have \(r > 1\) and if ‘X’ is one of the exceptional types ‘E’, ‘F’ or ‘G’ then \(r\) is limited to only a few possibilities. The exceptional types are:

['G', 2], ['F', 4], ['E', 6], ['E', 7] or ['E', 8].

A simply-connected semisimple group is a direct product of simple Lie groups, which are given by the following table. The integer \(r\) is called the rank, and is the dimension of the maximal torus.

Here are the Lie groups corresponding to the classical types:

compact group	complex analytic group	Cartan type
\(SU(r+1)\)	\(SL(r+1,\CC)\)	\(A_r\)
\(spin(2r+1)\)	\(spin(2r+1,\CC)\)	\(B_r\)
\(Sp(2r)\)	\(Sp(2r,\CC)\)	\(C_r\)
\(spin(2r)\)	\(spin(2r,\CC)\)	\(D_r\)

You may create these Cartan types and their Dynkin diagrams as follows:

Sage

sage: ct = CartanType("D5"); ct
['D', 5]

Python

>>> from sage.all import *
>>> ct = CartanType("D5"); ct
['D', 5]

Here "D5" is an abbreviation for ['D',5]. The group \(spin(n)\) is the simply-connected double cover of the orthogonal group \(SO(n)\).

Dual Cartan types

Every Cartan type has a dual, which you can get from within Sage:

Sage

sage: CartanType("B4").dual()
['C', 4]

Python

>>> from sage.all import *
>>> CartanType("B4").dual()
['C', 4]

Types other than \(B_r\) and \(C_r\) for \(r > 2\) are self-dual in the sense that the dual is isomorphic to the original type; however the isomorphism of a Cartan type with its dual might relabel the vertices. We can see this as follows:

Sage

sage: CartanType("F4").dynkin_diagram()
O---O=>=O---O
1   2   3   4
F4
sage: CartanType("F4").dual()
['F', 4] relabelled by {1: 4, 2: 3, 3: 2, 4: 1}
sage: CartanType("F4").dual().dynkin_diagram()
O---O=>=O---O
4   3   2   1
F4 relabelled by {1: 4, 2: 3, 3: 2, 4: 1}

Python

>>> from sage.all import *
>>> CartanType("F4").dynkin_diagram()
O---O=>=O---O
1   2   3   4
F4
>>> CartanType("F4").dual()
['F', 4] relabelled by {1: 4, 2: 3, 3: 2, 4: 1}
>>> CartanType("F4").dual().dynkin_diagram()
O---O=>=O---O
4   3   2   1
F4 relabelled by {1: 4, 2: 3, 3: 2, 4: 1}

Reducible Cartan types

If \(G\) is a Lie group of finite index in \(G_1 \times G_2\), where \(G_1\) and \(G_2\) are Lie groups of positive dimension, then \(G\) is called reducible. In this case, the root system of \(G\) is the disjoint union of the root systems of \(G_1\) and \(G_2\), which lie in orthogonal subspaces of the ambient space of the weight space of \(G\). The Cartan type of \(G\) is thus reducible.

Reducible Cartan types are supported in Sage as follows:

Sage

sage: RootSystem("A1xA1")
Root system of type A1xA1
sage: WeylCharacterRing("A1xA1")
The Weyl Character Ring of Type A1xA1 with Integer Ring coefficients

Python

>>> from sage.all import *
>>> RootSystem("A1xA1")
Root system of type A1xA1
>>> WeylCharacterRing("A1xA1")
The Weyl Character Ring of Type A1xA1 with Integer Ring coefficients

Low dimensional Cartan types

There are some isomorphisms that occur in low degree.

Cartan Type	Group	Equivalent Type	Isomorphic Group
\(B_2\)	\(spin(5)\)	\(C_2\)	\(Sp(4)\)
\(D_3\)	\(spin(6)\)	\(A_3\)	\(SL(4)\)
\(D_2\)	\(spin(4)\)	\(A1 \times A_1\)	\(SL(2)\times SL(2)\)
\(B_1\)	\(spin(3)\)	\(A_1\)	\(SL(2)\)
\(C_1\)	\(Sp(2)\)	\(A_1\)	\(SL(2)\)

Sometimes the redundant Cartan types such as \(D_3\) and \(D_2\) are excluded from the list of Cartan types. However Sage allows them since excluding them leads to exceptions having to be made in algorithms. A better approach, which is followed by Sage, is to allow the redundant Cartan types, but to implement the isomorphisms explicitly as special cases of branching rules. The utility of this approach may be seen by considering that the rank one group \(SL(2)\) has different natural weight lattices realizations depending on whether we consider it to be \(SL(2)\), \(spin(2)\) or \(Sp(2)\):

Sage

sage: RootSystem("A1").ambient_space().simple_roots()
Finite family {1: (1, -1)}
sage: RootSystem("B1").ambient_space().simple_roots()
Finite family {1: (1)}
sage: RootSystem("C1").ambient_space().simple_roots()
Finite family {1: (2)}

Python

>>> from sage.all import *
>>> RootSystem("A1").ambient_space().simple_roots()
Finite family {1: (1, -1)}
>>> RootSystem("B1").ambient_space().simple_roots()
Finite family {1: (1)}
>>> RootSystem("C1").ambient_space().simple_roots()
Finite family {1: (2)}

Relabeled Cartan types

By default Sage uses the labeling of the Dynkin diagram from [Bourbaki46]. There is another labeling of the vertices due to Dynkin. Most of the literature follows [Bourbaki46], though [Kac] follows Dynkin.

If you need to use Dynkin’s labeling, you should be aware that Sage does support relabeled Cartan types. See the documentation in sage.combinat.root_system.type_relabel for further information.

Standard realizations of the ambient spaces

These realizations follow the Appendix in [Bourbaki46]. See the Root system plot tutorial for how to visualize them.

Type A

For type \(A_r\) we use an \(r+1\) dimensional ambient space. This means that we are modeling the Lie group \(U(r+1)\) or \(GL(r+1,\CC)\) rather than \(SU(r+1)\) or \(SL(r+1,\CC)\). The ambient space is identified with \(\mathbf{Q}^{r+1}\):

Sage

sage: RootSystem("A3").ambient_space().simple_roots()
Finite family {1: (1, -1, 0, 0), 2: (0, 1, -1, 0), 3: (0, 0, 1, -1)}
sage: RootSystem("A3").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0, 0), 2: (1, 1, 0, 0), 3: (1, 1, 1, 0)}
sage: RootSystem("A3").ambient_space().rho()
(3, 2, 1, 0)

Python

>>> from sage.all import *
>>> RootSystem("A3").ambient_space().simple_roots()
Finite family {1: (1, -1, 0, 0), 2: (0, 1, -1, 0), 3: (0, 0, 1, -1)}
>>> RootSystem("A3").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0, 0), 2: (1, 1, 0, 0), 3: (1, 1, 1, 0)}
>>> RootSystem("A3").ambient_space().rho()
(3, 2, 1, 0)

The dominant weights consist of integer \(r+1\)-tuples \(\lambda = (\lambda_1,\dots,\lambda_{r+1})\) such that \(\lambda_1 \ge \dots \ge \lambda_{r+1}\).

See SL versus GL for further remarks about Type A.

Type B

For the remaining classical Cartan types \(B_r\), \(C_r\) and \(D_r\) we use an \(r\)-dimensional ambient space:

Sage

sage: RootSystem("B3").ambient_space().simple_roots()
Finite family {1: (1, -1, 0), 2: (0, 1, -1), 3: (0, 0, 1)}
sage: RootSystem("B3").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0), 2: (1, 1, 0), 3: (1/2, 1/2, 1/2)}
sage: RootSystem("B3").ambient_space().rho()
(5/2, 3/2, 1/2)

Python

>>> from sage.all import *
>>> RootSystem("B3").ambient_space().simple_roots()
Finite family {1: (1, -1, 0), 2: (0, 1, -1), 3: (0, 0, 1)}
>>> RootSystem("B3").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0), 2: (1, 1, 0), 3: (1/2, 1/2, 1/2)}
>>> RootSystem("B3").ambient_space().rho()
(5/2, 3/2, 1/2)

This is the Cartan type of \(spin(2r+1)\). The last fundamental weight (1/2, 1/2, ..., 1/2) is the highest weight of the \(2^r\) dimensional spin representation. All the other fundamental representations factor through the homomorphism \(spin(2r+1) \to SO(2r+1)\) and are representations of the orthogonal group.

The dominant weights consist of \(r\)-tuples of integers or half-integers \((\lambda_1,\dots,\lambda_r)\) such that \(\lambda_1 \ge \lambda_2 \dots \ge \lambda_r \ge 0\), and such that the differences \(\lambda_i - \lambda_j \in \mathbf{Z}\).

Type C

Sage

sage: RootSystem("C3").ambient_space().simple_roots()
Finite family {1: (1, -1, 0), 2: (0, 1, -1), 3: (0, 0, 2)}
sage: RootSystem("C3").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0), 2: (1, 1, 0), 3: (1, 1, 1)}
sage: RootSystem("C3").ambient_space().rho()
(3, 2, 1)

Python

>>> from sage.all import *
>>> RootSystem("C3").ambient_space().simple_roots()
Finite family {1: (1, -1, 0), 2: (0, 1, -1), 3: (0, 0, 2)}
>>> RootSystem("C3").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0), 2: (1, 1, 0), 3: (1, 1, 1)}
>>> RootSystem("C3").ambient_space().rho()
(3, 2, 1)

This is the Cartan type of the symplectic group \(Sp(2r)\).

The dominant weights consist of \(r\)-tuples of integers \(\lambda = (\lambda_1,\dots,\lambda_{r+1})\) such that \(\lambda_1 \ge \cdots \ge \lambda_r \ge 0\).

Type D

Sage

sage: RootSystem("D4").ambient_space().simple_roots()
Finite family {1: (1, -1, 0, 0), 2: (0, 1, -1, 0), 3: (0, 0, 1, -1), 4: (0, 0, 1, 1)}
sage: RootSystem("D4").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0, 0), 2: (1, 1, 0, 0), 3: (1/2, 1/2, 1/2, -1/2), 4: (1/2, 1/2, 1/2, 1/2)}
sage: RootSystem("D4").ambient_space().rho()
(3, 2, 1, 0)

Python

>>> from sage.all import *
>>> RootSystem("D4").ambient_space().simple_roots()
Finite family {1: (1, -1, 0, 0), 2: (0, 1, -1, 0), 3: (0, 0, 1, -1), 4: (0, 0, 1, 1)}
>>> RootSystem("D4").ambient_space().fundamental_weights()
Finite family {1: (1, 0, 0, 0), 2: (1, 1, 0, 0), 3: (1/2, 1/2, 1/2, -1/2), 4: (1/2, 1/2, 1/2, 1/2)}
>>> RootSystem("D4").ambient_space().rho()
(3, 2, 1, 0)

This is the Cartan type of \(spin(2r)\). The last two fundamental weights are the highest weights of the two \(2^{r-1}\)-dimensional spin representations.

The dominant weights consist of \(r\)-tuples of integers \(\lambda = (\lambda_1,\dots,\lambda_{r+1})\) such that \(\lambda_1 \ge \cdots \ge \lambda_{r-1} \ge |\lambda_r|\).

Exceptional Types

We leave the reader to examine the exceptional types. You can use Sage to list the fundamental dominant weights and simple roots.

Weights and the ambient space

Let \(G\) be a reductive complex analytic group. Let \(T\) be a maximal torus, \(\Lambda = X^{\ast} (T)\) be its group of analytic characters. Then \(T \cong (\CC^{\times})^r\) for some \(r\) and \(\Lambda \cong \ZZ^r\).

Example 1: Let \(G = \hbox{GL}_{r+1} (\CC)\). Then \(T\) is the diagonal subgroup and \(X^{\ast} (T) \cong \ZZ^{r+1}\). If \(\lambda = (\lambda_1, \dots, \lambda_n)\) then \(\lambda\) is identified with the rational character

\[\begin{split}{\bf t} = \left(\begin{array}{ccc} t_1 & & \\ & \ddots & \\ & & t_n \end{array}\right) \longmapsto \prod t_i^{\lambda_i}.\end{split}\]

Example 2: Let \(G = \hbox{SL}_{r+1} (\CC)\). Again \(T\) is the diagonal subgroup but now if \(\lambda \in \ZZ^{\Delta} = \{(d, \cdots, d) | d \in \ZZ\} \subseteq \ZZ^{r+1}\) then \(\prod t_i^{\lambda_i} = \det ({\bf t})^d = 1\), so \(X^{\ast} (T) \cong \ZZ^{r+1} /\ZZ^{\Delta} \cong \ZZ^r\).

• Elements of \(\Lambda\) are called weights.

• If \(\pi: G \to GL(V)\) is any representation we may restrict \(\pi\) to \(T\). Then the characters of \(T\) that occur in this restriction are called the weights of \(\pi\).

• \(G\) acts on its Lie algebra by conjugation (the adjoint representation).

• The nonzero weights of the adjoint representation are called roots.

• The ambient space of \(\Lambda\) is \(\QQ \otimes \Lambda\).

The root system

As we have mentioned, \(G\) acts on its complexified Lie algebra \(\mathfrak{g}_{\CC}\) by the adjoint representation. The zero weight space \(\mathfrak{g}_{\CC}(0)\) is just the Lie algebra of \(T\) itself. The other nonzero weights each appear with multiplicity one and form an interesting configuration of vectors called the root system \(\Phi\).

It is convenient to partition \(\Phi\) into two sets \(\Phi^+\) and \(\Phi^-\) such that \(\Phi^+\) consists of all roots lying on one side of a hyperplane. Often we arrange things so that \(G\) is embedded in \(GL(n,\CC)\) in such a way that the positive weights correspond to upper triangular matrices. Thus if \(\alpha\) is a positive root, its weight space \(\mathfrak{g}_{\CC}(\alpha)\) is spanned by a vector \(X_\alpha\), and the exponential of this eigenspace in \(G\) is a one-parameter subgroup of unipotent matrices. It is always possible to arrange that this one-parameter subgroup consists of upper triangular matrices.

If \(\alpha\) is a positive root that cannot be decomposed as a sum of other positive roots, then \(\alpha\) is called a simple root. If \(G\) is semisimple of rank \(r\), then \(r\) is the number of positive roots. Let \(\alpha_1, \ldots, \alpha_r\) be these.

The Weyl group

Let \(G\) be a complex analytic group. Let \(T\) be a maximal torus, and let \(N(T)\) be its normalizer. Let \(W = N(T)/T\) be the Weyl group. It acts on \(T\) by conjugation; therefore it acts on the weight lattice \(\Lambda\) and its ambient space. The ambient space admits an inner product that is invariant under this action. Let \((v | w)\) denote this inner product. If \(\alpha\) is a root let \(r_\alpha\) denote the reflection in the hyperplane of the ambient space that is perpendicular to \(\alpha\). If \(\alpha = \alpha_i\) is a simple root, then we use the notation \(s_i\) to denote \(r_\alpha\).

Then \(s_1, \ldots, s_r\) generate \(W\), which is a Coxeter group. This means that it is generated by elements \(s_i\) of order two and that if \(m(i,j)\) is the order of \(s_i s_j\), then

\[W = \left\langle s_i \mid s_i^2=1, (s_i s_j)^{m(i,j)} = 1 \right\rangle\]

is a presentation. An important function \(\ell : W \to \ZZ\) is the length function, where \(\ell(w)\) is the length of the shortest decomposition of \(w\) into a product of simple reflections.

The dual root system

The coroots are certain linear functionals on the ambient space that also form a root system. Since the ambient space admits a \(W\)-invariant inner product \((\ |\ )\), they may be identified with elements of the ambient space itself. Then they are proportional to the roots, though if the roots have different lengths, long roots correspond to short coroots and conversely. The coroot corresponding to the root \(\alpha\) is

\[\alpha^\vee = \frac{2\alpha}{(\alpha | \alpha)}.\]

We can also describe the natural pairing between coroots and roots using this invariant inner product as

\[\langle \alpha^{\vee}, \beta \rangle = 2 \frac{(\alpha | \beta)}{(\alpha | \alpha)}.\]

The Dynkin diagram

The Dynkin diagram is a graph whose vertices are in bijection with the set simple roots. We connect the vertices corresponding to roots that are not orthogonal. Usually two such roots (vertices) make an angle of \(2\pi/3\), in which case we connect them with a single bond. Occasionally they may make an angle of \(3\pi/4\) in which case we connect them with a double bond, or \(5\pi/6\) in which case we connect them with a triple bond. If the bond is single, the roots have the same length with respect to the inner product on the ambient space. In the case of a double or triple bond, the two simple roots in questions have different length, and the bond is drawn as an arrow from the long root to the short root. Only the exceptional group \(G_2\) has a triple bond.

There are various ways to get the Dynkin diagram in Sage:

Sage

sage: DynkinDiagram("D5")
        O 5
        |
        |
O---O---O---O
1   2   3   4
D5
sage: ct = CartanType("E6"); ct
['E', 6]
sage: ct.dynkin_diagram()
        O 2
        |
        |
O---O---O---O---O
1   3   4   5   6
E6
sage: B4 = WeylCharacterRing("B4"); B4
The Weyl Character Ring of Type B4 with Integer Ring coefficients
sage: B4.dynkin_diagram()
O---O---O=>=O
1   2   3   4
B4
sage: RootSystem("G2").dynkin_diagram()
  3
O=<=O
1   2
G2

Python

>>> from sage.all import *
>>> DynkinDiagram("D5")
        O 5
        |
        |
O---O---O---O
1   2   3   4
D5
>>> ct = CartanType("E6"); ct
['E', 6]
>>> ct.dynkin_diagram()
        O 2
        |
        |
O---O---O---O---O
1   3   4   5   6
E6
>>> B4 = WeylCharacterRing("B4"); B4
The Weyl Character Ring of Type B4 with Integer Ring coefficients
>>> B4.dynkin_diagram()
O---O---O=>=O
1   2   3   4
B4
>>> RootSystem("G2").dynkin_diagram()
  3
O=<=O
1   2
G2

The Cartan matrix

Consider the natural pairing \(\langle\ ,\ \rangle\) between coroots and roots, then the defining matrix of this pairing is called the Cartan matrix. That is to say, the Cartan matrix \(A = (a_{ij})_{ij}\) is given by

\[a_{ij} = \langle \alpha_i^{\vee}, \alpha_j \rangle.\]

This uniquely corresponds to a root system/Dynkin diagram/Lie group.

We note that we have made a convention choice, and the opposite convention corresponds to taking the transpose of the Cartan matrix.

Fundamental weights and the Weyl vector

There are certain weights \(\omega_1, \ldots, \omega_r\) that:

\[\langle \omega_j, \alpha_i \rangle = 2 \frac{( \alpha_i | \omega_j )}{( \alpha_i | \alpha_i ) } = \delta_{ij}.\]

If \(G\) is semisimple then these are uniquely determined, whereas if \(G\) is reductive but not semisimple we may choose them conveniently.

Let \(\rho\) be the sum of the fundamental dominant weights. If \(G\) is semisimple, then \(\rho\) is half the sum of the positive roots. In case \(G\) is not semisimple, we have noted, the fundamental weights are not completely determined by the inner product condition given above. If we make a different choice, then \(\rho\) is altered by a vector that is orthogonal to all roots. This is a harmless change for many purposes such as the Weyl character formula.

In Sage, this issue arises only for Cartan type \(A_r\). See SL versus GL.

Representations and characters

Let \(T\) be a maximal torus and \(\Lambda = X^{\ast} (T)\) be the group of rational characters. Then \(\Lambda \cong \ZZ^r\).

• Recall that elements of \(\Lambda \cong \ZZ^r\) are called weights.

• The Weyl group \(W = N(T)/T\) acts on \(T\), hence on \(\Lambda\) and its ambient space by conjugation.

• The ambient space \(\QQ \otimes X^{\ast} (T) \cong \QQ^r\) has a fundamental domain \(\mathcal{C}^+\) for the Weyl group \(W\) called the positive Weyl chamber. Weights in \(\mathcal{C}^+\) are called dominant.

• Then \(\mathcal{C}^+\) consists of all vectors such that \((\alpha | v) \geq 0\) for all positive roots \(\alpha\).

• It is useful to embed \(\Lambda\) in \(\RR^r\) and consider weights as lattice points.

• If \((\pi, V)\) is a representation then restricting to \(T\), the module \(V\) decomposes into a direct sum of weight eigenspaces \(V(\mu)\) with multiplicity \(m (\mu)\) for weight \(\mu\).

• There is a unique highest weight \(\lambda\) with respect to the partial order. We have \(\lambda \in \mathcal{C}\) and \(m (\lambda) = 1\).

• \(V \longleftrightarrow \lambda\) gives a bijection between irreducible representations and weights \(\lambda\) in \(\mathcal{C}^+\).

Assuming that \(G\) is simply-connected (or more generally, reductive with a simply-connected derived group) every dominant weight \(\lambda\) is the highest weight of a unique irreducible representation \(\pi_\lambda\), and \(\lambda \mapsto \pi_\lambda\) gives a parametrization of the isomorphism classes of irreducible representations of \(G\) by the dominant weights.

The character of \(\pi_\lambda\) is the function \(\chi_\lambda(g) = tr(\pi_\lambda(g))\). It is determined by its values on \(T\). If \(\mathbf(z) \in T\) and \(\mu \in \Lambda\), let us write \(\mathbf{z}^\mu\) for the value of \(\mu\) on \(\mathbf{z}\). Then the character:

\[\chi_\lambda(\mathbf{z}) = \sum_{\mu\in\Lambda}m(\mu)\,\mathbf{z}^\lambda.\]

Sometimes this is written

\[\chi_\lambda = \sum_{\mu\in\Lambda}m(\mu)\,e^\lambda.\]

The meaning of \(e^\lambda\) is subject to interpretation, but we may regard it as the image of the additive group \(\Lambda\) in its group algebra. The character is then regarded as an element of this ring, the group algebra of \(\Lambda\).

Representations: an example

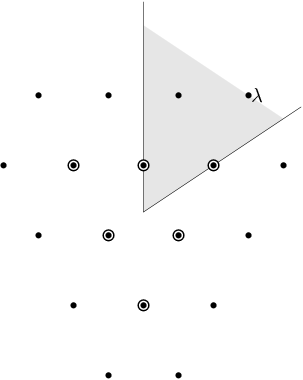
In this example, \(G = \hbox{SL}(3,\CC)\). We have drawn the weights of an irreducible representation with highest weight \(\lambda\). The shaded region is \(\mathcal{C}^+\). \(\lambda\) is a dominant weight, and the labeled vertices are the weights with positive multiplicity in \(V(\lambda)\). The weights weights on the outside have \(m(\mu) = 1\), while the six interior weights (with double circles) have \(m(\mu) = 2\).

Partitions and Schur polynomials

The considerations of this section are particular to type \(A\). We review the relationship between characters of \(GL(n,\CC)\) and symmetric function theory.

A partition \(\lambda\) is a sequence of descending nonnegative integers:

\[\lambda = (\lambda_1, \lambda_2, \dots, \lambda_n), \qquad \lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_n \ge 0.\]

We do not distinguish between two partitions if they differ only by some trailing zeros, so \((3, 2) = (3, 2, 0)\). If \(l\) is the last integer such that \(\lambda_l > 0\) then we say that \(l\) is the length of \(\lambda\). If \(k = \sum \lambda_i\) then we say that \(\lambda\) is a partition of \(k\) and write \(\lambda \vdash k\).

A partition of length \(\le n=r+1\) is therefore a dominant weight of type ['A',r]. Not every dominant weight is a partition, since the coefficients in a dominant weight could be negative. Let us say that an element \(\mu = (\mu_1, \mu_2, \cdots, \mu_n)\) of the ['A',r] root lattice is effective if the \(\mu_i \ge 0\). Thus an effective dominant weight of ['A',r] is a partition of length \(\le n\), where \(n = r+1\).

Let \(\lambda\) be a dominant weight, and let \(\chi_\lambda\) be the character of \(GL(n,\CC)\) with highest weight \(\lambda\). If \(k\) is any integer we may consider the weight \(\mu = (\lambda_1+k,\dots,\lambda_n+k)\) obtained by adding \(k\) to each entry. Then \(\chi_{\mu} = \det^k \otimes \chi_\lambda\). Clearly by choosing \(k\) large enough, we may make \(\mu\) effective.

So the characters of irreducible representations of \(GL(n,\CC)\) do not all correspond to partitions, but the characters indexed by partitions (effective dominant weights) are enough that we can write any character \(\det^{-k}\chi_{\mu}\) where \(\mu\) is a partition. If we take \(k = -\lambda_n\) we could also arrange that the last entry in \(\lambda\) is zero.

If \(\lambda\) is an effective dominant weight, then every weight that appears in \(\chi_\lambda\) is effective. (Indeed, it lies in the convex hull of \(w(\lambda)\) where \(w\) runs through the Weyl group \(W = S_n\).) This means that if

\[\begin{split}g = \left(\begin{array}{ccc} z_1 \\ & \ddots \\ && z_n \end{array}\right) \in GL(n,\CC)\end{split}\]

then \(\chi_\lambda(g)\) is a polynomial in the eigenvalues of \(g\). This is the Schur polynomial \(s_\lambda(z_1, \ldots, z_n)\).

Affine Cartan types

There are also affine Cartan types, which correspond to (infinite dimensional) affine Lie algebras. There are affine Cartan types of the form [`X`, r, 1] if X=A,B,C,D,E,F,G and [`X`, r] is an ordinary Cartan type. There are also twisted affine types of the form [X, r, k], where \(k = 2\) or \(3\) if the Dynkin diagram of the ordinary Cartan type [X, r] has an automorphism of degree \(k\). When \(k = 1\), the affine Cartan type is said to be untwisted.

Illustrating some of the methods available for the untwisted affine Cartan type ['A', 4, 1]:

Sage

sage: ct = CartanType(['A',4,1]); ct
['A', 4, 1]
sage: ct.dual()
['A', 4, 1]
sage: ct.classical()
['A', 4]
sage: ct.dynkin_diagram()
0
O-----------+
|           |
|           |
O---O---O---O
1   2   3   4
A4~

Python

>>> from sage.all import *
>>> ct = CartanType(['A',Integer(4),Integer(1)]); ct
['A', 4, 1]
>>> ct.dual()
['A', 4, 1]
>>> ct.classical()
['A', 4]
>>> ct.dynkin_diagram()
0
O-----------+
|           |
|           |
O---O---O---O
1   2   3   4
A4~

The twisted affine Cartan types are relabeling of the duals of certain untwisted Cartan types:

Sage

sage: CartanType(['A',3,2])
['B', 2, 1]^*
sage: CartanType(['D',4,3])
['G', 2, 1]^* relabelled by {0: 0, 1: 2, 2: 1}

Python

>>> from sage.all import *
>>> CartanType(['A',Integer(3),Integer(2)])
['B', 2, 1]^*
>>> CartanType(['D',Integer(4),Integer(3)])
['G', 2, 1]^* relabelled by {0: 0, 1: 2, 2: 1}

The affine root and the extended Dynkin diagram

For the extended Dynkin diagram, we add one negative root \(\alpha_0\). For the untwisted types, this is the root whose negative is the highest weight in the adjoint representation. Sometimes this is called the affine root. We make the Dynkin diagram as before by measuring the angles between the roots. This extended Dynkin diagram is useful for many purposes, such as finding maximal subgroups and for describing the affine Weyl group.

In particular, the hyperplane for the reflection \(r_0\), used in generating the affine Weyl group, is translated off the origin (so it becomes an affine hyperplane). Now the root system is not described as linear transformations on an Euclidean space, but instead by affine transformations. Thus the dominant chamber has finite volume and tiles the Eucledian space. Moreover, each such tile corresponds to a unique element in the affine Weyl group.

The extended Dynkin diagram may be obtained as the Dynkin diagram of the corresponding untwisted affine type:

Sage

sage: ct = CartanType("E6"); ct
['E', 6]
sage: ct.affine()
['E', 6, 1]
sage: ct.affine() == CartanType(['E',6,1])
True
sage: ct.affine().dynkin_diagram()
        O 0
        |
        |
        O 2
        |
        |
O---O---O---O---O
1   3   4   5   6
E6~

Python

>>> from sage.all import *
>>> ct = CartanType("E6"); ct
['E', 6]
>>> ct.affine()
['E', 6, 1]
>>> ct.affine() == CartanType(['E',Integer(6),Integer(1)])
True
>>> ct.affine().dynkin_diagram()
        O 0
        |
        |
        O 2
        |
        |
O---O---O---O---O
1   3   4   5   6
E6~

The extended Dynkin diagram is also a method of the WeylCharacterRing:

Sage

sage: WeylCharacterRing("E7").extended_dynkin_diagram()
            O 2
            |
            |
O---O---O---O---O---O---O
0   1   3   4   5   6   7
E7~

Python

>>> from sage.all import *
>>> WeylCharacterRing("E7").extended_dynkin_diagram()
            O 2
            |
            |
O---O---O---O---O---O---O
0   1   3   4   5   6   7
E7~

We note the following important distinctions from the classical cases:

• The affine Weyl groups are all infinite.

• Type \(A_1^{(1)}\) has two anti-parallel roots with distinct reflections. The Dynkin diagram in this case is represented by a double bond with arrows going in both directions.

Twisted affine root systems

For the construction of \(\alpha_0\) in the twisted types, we refer the reader to Chapter 8 of [Kac]. As mentioned above, most twisted types can be constructed by taking the dual root system of an untwisted type. However the type \(A_{2n}^{(2)}\) root system can only be constructed by the twisting procedure defined in [Kac]. It has the following properties:

• The Dynkin diagram of type \(A_2^{(2)}\) has a quadruple bond with an arrow pointing from the short root to the long root.

• Type \(A_{2n}^{(2)}\) for \(n > 1\) has 3 different root lengths.

Further Generalizations

If a root system (on an Euclidean space) has only the angles \(\pi/2, 2\pi/3, 3\pi/4, 5\pi/6\) between its roots, then we call the root system crystallographic (on Wikipedia article Root_system, this condition is called integrality since for any two roots we have \(\langle \beta, \alpha \rangle \in \ZZ\)). So if we look at the reflection group generated by the roots (this is not a Weyl group), we get general Coxeter groups (with non-infinite labels) and non-crystallographic Coxeter groups are not connected with Lie theory.

However we can generalize Dynkin diagrams (equivalently Cartan matrices) to have all its edges labelled by \((a, b)\) where \(a, b \in \ZZ_{>0}\) and corresponds to having \(a\) arrows point one way and \(b\) arrows pointing the other. For example in type \(A_{1}^{(1)}\), we have one edge of \((2, 2)\), or in type \(A_{2}^{(2)}\), we have one edge of \((1, 4)\) (equivalently \((4, 1)\)). These edge label between \(i\) and \(j\) corresponds to the entries \(a_{ij}\) and \(a_{ji}\) in the Cartan matrix. These are used to construct a class of (generally infinite dimensional) Lie algebras called Kac-Moody (Lie) algebras, which in turn are used to construct quantum groups. We refer the reader to [Kac] and [HongKang2002] for more information.