Tutorial: Programming in Python and Sage#

Author: Florent Hivert <florent.hivert@univ-rouen.fr>, Franco Saliola <saliola@gmail.com>, et al.

This tutorial is an introduction to basic programming in Python and Sage, for readers with elementary notions of programming but not familiar with the Python language. It is far from exhaustive. For a more complete tutorial, have a look at the Python Tutorial. Also Python’s documentation and in particular the standard library can be useful.

A more advanced tutorial presents the notions of objects and classes in Python.

Here are further resources to learn Python:

Learn Python in 10 minutes ou en français Python en 10 minutes
Dive into Python is a Python book for experienced programmers. Also available in other languages.
Discover Python is a series of articles published in IBM’s developerWorks technical resource center.

Data structures#

In Python, typing is dynamic; there is no such thing as declaring variables. The function type() returns the type of an object obj. To convert an object to a type typ just write typ(obj) as in int("123"). The command isinstance(ex, typ) returns whether the expression ex is of type typ. Specifically, any value is an instance of a class and there is no difference between classes and types.

The symbol = denotes the affectation to a variable; it should not be confused with == which denotes mathematical equality. Inequality is !=.

The standard types are bool, int, list, tuple, set, dict, str.

The type bool (booleans) has two values: True and False. The boolean operators are denoted by their names or, and, not.
The Python type int is used to represent integers of limited size. To handle arbitrary large integers with exact arithmetic, Sage uses its own type named Integer.

A list is a data structure which groups values. It is constructed using brackets as in [1, 3, 4]. The range() function creates integer lists. One can also create lists using list comprehension:

[ <expr> for <name> in <iterable> (if <condition>) ]

For example:

Sage

sage: [ i^2 for i in range(10) if i % 2 == 0 ]
[0, 4, 16, 36, 64]

Python

>>> from sage.all import *
>>> [ i**Integer(2) for i in range(Integer(10)) if i % Integer(2) == Integer(0) ]
[0, 4, 16, 36, 64]

A tuple is very similar to a list; it is constructed using parentheses. The empty tuple is obtained by () or by the constructor tuple. If there is only one element, one has to write (a,). A tuple is immutable (one cannot change it) but it is hashable (see below). One can also create tuples using comprehensions:
Sage
sage: tuple(i^2 for i in range(10) if i % 2 == 0) (0, 4, 16, 36, 64)
Python
>>> from sage.all import * >>> tuple(i**Integer(2) for i in range(Integer(10)) if i % Integer(2) == Integer(0)) (0, 4, 16, 36, 64)

A set is a data structure which contains values without multiplicities or order. One creates it from a list (or any iterable) with the constructor set. The elements of a set must be hashable:

Sage

sage: set([2,2,1,4,5])
{1, 2, 4, 5}

sage: set([ [1], [2] ])
Traceback (most recent call last):
...
TypeError: unhashable type: 'list'

Python

>>> from sage.all import *
>>> set([Integer(2),Integer(2),Integer(1),Integer(4),Integer(5)])
{1, 2, 4, 5}

>>> set([ [Integer(1)], [Integer(2)] ])
Traceback (most recent call last):
...
TypeError: unhashable type: 'list'

A dictionary is an association table, which associates values to keys. Keys must be hashable. One creates dictionaries using the constructor dict, or using the syntax:

{key1 : value1, key2 : value2 ...}

For example:

Sage

sage: age = {'toto' : 8, 'mom' : 27}; age
{'mom': 27, 'toto': 8}

Python

>>> from sage.all import *
>>> age = {'toto' : Integer(8), 'mom' : Integer(27)}; age
{'mom': 27, 'toto': 8}

Quotes (simple ' ' or double " ") enclose character strings. One can concatenate them using +.
For lists, tuples, strings, and dictionaries, the indexing operator is written l[i]. For lists, tuples, and strings one can also uses slices as l[:], l[:b], l[a:], or l[a:b]. Negative indices start from the end.
The len() function returns the number of elements of a list, a tuple, a set, a string, or a dictionary. One writes x in C to tests whether x is in C.
Finally there is a special value called None to denote the absence of a value.

Control structures#

In Python, there is no keyword for the beginning and the end of an instructions block. Blocks are delimited solely by means of indentation. Most of the time a new block is introduced by :. Python has the following control structures:

Conditional instruction:

if <condition>:
    <instruction sequence>
[elif <condition>:
    <instruction sequence>]*
[else:
    <instruction sequence>]

Inside expression exclusively, one can write:
```
<value> if <condition> else <value>
```

Iterative instructions:

for <name> in <iterable>:
    <instruction sequence>
[else:
    <instruction sequence>]

while <condition>:
    <instruction sequence>
[else:
    <instruction sequence>]

The else block is executed at the end of the loop if the loop is ended normally, that is neither by a break nor an exception.

In a loop, continue jumps to the next iteration.
An iterable is an object which can be iterated through. Iterable types include lists, tuples, dictionaries, and strings.
An error (also called exception) is raised by:
```
raise <ErrorType>[("error message")]
```
Usual errors include ValueError and TypeError.

Functions#

Note

Python functions vs. mathematical functions

In what follows, we deal with functions is the sense of programming languages. Mathematical functions, as manipulated in calculus, are handled by Sage in a different way. In particular it doesn’t make sense to do mathematical manipulation such as additions or derivations on Python functions.

One defines a function using the keyword def as:

def <name>(<argument list>):
     <instruction sequence>

The result of the function is given by the instruction return. Very short functions can be created anonymously using lambda (remark that there is no instruction return here):

lambda <arguments>: <expression>

Note

Functional programming

Functions are objects as any other objects. One can assign them to variables or return them. For details, see the tutorial on Functional Programming for Mathematicians.

Exercises#

Tuples#

A tuple is an immutable list. That is, it cannot be changed once it is created. This can be useful for code safety and foremost because it makes tuple hashable. To create a tuple, use parentheses instead of brackets:

Sage

sage: t = (3, 5, [3,1], (17,[2,3],17), 4)
sage: t
(3, 5, [3, 1], (17, [2, 3], 17), 4)

Python

>>> from sage.all import *
>>> t = (Integer(3), Integer(5), [Integer(3),Integer(1)], (Integer(17),[Integer(2),Integer(3)],Integer(17)), Integer(4))
>>> t
(3, 5, [3, 1], (17, [2, 3], 17), 4)

To create a singleton tuple, a comma is required to resolve the ambiguity:

Sage

sage: (1)
1
sage: (1,)
(1,)

Python

>>> from sage.all import *
>>> (Integer(1))
1
>>> (Integer(1),)
(1,)

We can create a tuple from a list, and vice-versa.

Sage

sage: tuple(range(5))
(0, 1, 2, 3, 4)

Python

>>> from sage.all import *
>>> tuple(range(Integer(5)))
(0, 1, 2, 3, 4)

Sage

sage: list(t)
[3, 5, [3, 1], (17, [2, 3], 17), 4]

Python

>>> from sage.all import *
>>> list(t)
[3, 5, [3, 1], (17, [2, 3], 17), 4]

Tuples behave like lists in many respects:

Operation	Syntax for lists	Syntax for tuples
Accessing a letter	`list[3]`	`tuple[3]`
Concatenation	`list1 + list2`	`tuple1 + tuple2`
Slicing	`list[3:17:2]`	`tuple[3:17:2]`
A reversed copy	`list[::-1]`	`tuple[::-1]`
Length	`len(list)`	`len(tuple)`

Trying to modify a tuple will fail:

Sage

sage: t = (5, 'a', 6/5)
sage: t
(5, 'a', 6/5)

Python

>>> from sage.all import *
>>> t = (Integer(5), 'a', Integer(6)/Integer(5))
>>> t
(5, 'a', 6/5)

Sage

sage: t[1] = 'b'
Traceback (most recent call last):
...
TypeError: 'tuple' object does not support item assignment

Python

>>> from sage.all import *
>>> t[Integer(1)] = 'b'
Traceback (most recent call last):
...
TypeError: 'tuple' object does not support item assignment

Dictionaries#

A dictionary is another built-in data type. Unlike lists, which are indexed by a range of numbers starting at 0, dictionaries are indexed by keys, which can be any immutable objects. Strings and numbers can always be keys (because they are immutable). Dictionaries are sometimes called “associative arrays” in other programming languages.

There are several ways to define dictionaries. One method is to use braces, {}, with comma-separated entries given in the form key:value:

Sage

sage: d = {3:17, 0.5:[4,1,5,2,3], 0:"goo", 3/2 : 17}
sage: d
{0: 'goo', 0.500000000000000: [4, 1, 5, 2, 3], 3/2: 17, 3: 17}

Python

>>> from sage.all import *
>>> d = {Integer(3):Integer(17), RealNumber('0.5'):[Integer(4),Integer(1),Integer(5),Integer(2),Integer(3)], Integer(0):"goo", Integer(3)/Integer(2) : Integer(17)}
>>> d
{0: 'goo', 0.500000000000000: [4, 1, 5, 2, 3], 3/2: 17, 3: 17}

A second method is to use the constructor dict which admits a list (or actually any iterable) of 2-tuples (key, value):

Sage

sage: dd = dict((i,i^2) for i in range(10))
sage: dd
{0: 0, 1: 1, 2: 4, 3: 9, 4: 16, 5: 25, 6: 36, 7: 49, 8: 64, 9: 81}

Python

>>> from sage.all import *
>>> dd = dict((i,i**Integer(2)) for i in range(Integer(10)))
>>> dd
{0: 0, 1: 1, 2: 4, 3: 9, 4: 16, 5: 25, 6: 36, 7: 49, 8: 64, 9: 81}

Dictionaries behave as lists and tuples for several important operations.

Operation	Syntax for lists	Syntax for dictionaries
Accessing elements	`list[3]`	`D["key"]`
Length	`len(list)`	`len(D)`
Modifying	`L[3] = 17`	`D["key"] = 17`
Deleting items	`del L[3]`	`del D["key"]`

Sage

sage: d[10]='a'
sage: d
{0: 'goo', 0.500000000000000: [4, 1, 5, 2, 3], 3/2: 17, 3: 17, 10: 'a'}

Python

>>> from sage.all import *
>>> d[Integer(10)]='a'
>>> d
{0: 'goo', 0.500000000000000: [4, 1, 5, 2, 3], 3/2: 17, 3: 17, 10: 'a'}

A dictionary can have the same value multiple times, but each key must only appear once and must be immutable:

Sage

sage: d = {3: 14, 4: 14}
sage: d
{3: 14, 4: 14}

Python

>>> from sage.all import *
>>> d = {Integer(3): Integer(14), Integer(4): Integer(14)}
>>> d
{3: 14, 4: 14}

Sage

sage: d = {3: 13, 3: 14}
sage: d
{3: 14}

Python

>>> from sage.all import *
>>> d = {Integer(3): Integer(13), Integer(3): Integer(14)}
>>> d
{3: 14}

Sage

sage: d = {[1,2,3] : 12}
Traceback (most recent call last):
...
TypeError: unhashable type: 'list'

Python

>>> from sage.all import *
>>> d = {[Integer(1),Integer(2),Integer(3)] : Integer(12)}
Traceback (most recent call last):
...
TypeError: unhashable type: 'list'

Another way to add items to a dictionary is with the update() method which updates the dictionary from another dictionary:

Sage

sage: d = {}
sage: d
{}

Python

>>> from sage.all import *
>>> d = {}
>>> d
{}

Sage

sage: d.update({10 : 'newvalue', 20: 'newervalue', 3: 14, 0.5:[1,2,3]})
sage: d
{0.500000000000000: [1, 2, 3], 3: 14, 10: 'newvalue', 20: 'newervalue'}

Python

>>> from sage.all import *
>>> d.update({Integer(10) : 'newvalue', Integer(20): 'newervalue', Integer(3): Integer(14), RealNumber('0.5'):[Integer(1),Integer(2),Integer(3)]})
>>> d
{0.500000000000000: [1, 2, 3], 3: 14, 10: 'newvalue', 20: 'newervalue'}

We can iterate through the keys, or values, or both, of a dictionary. Note that, internally, there is no sorting of keys done. In general, the order of keys/values will depend on memory locations can and will differ between different computers and / or repeated runs on the same computer. However, Sage sort the dictionary entries by key when printing the dictionary specifically to make the docstrings more reproducible. However, the Python methods keys() and values() do not sort for you. If you want your output to be reproducible, then you have to sort it first just like in the examples below:

Sage

sage: d = {10 : 'newvalue', 20: 'newervalue', 3: 14, 0.5:(1,2,3)}

Python

>>> from sage.all import *
>>> d = {Integer(10) : 'newvalue', Integer(20): 'newervalue', Integer(3): Integer(14), RealNumber('0.5'):(Integer(1),Integer(2),Integer(3))}

Sage

sage: sorted([key for key in d])
[0.500000000000000, 3, 10, 20]

Python

>>> from sage.all import *
>>> sorted([key for key in d])
[0.500000000000000, 3, 10, 20]

Sage

sage: d.keys()   # random order
[0.500000000000000, 10, 3, 20]
sage: sorted(d.keys())
[0.500000000000000, 3, 10, 20]

Python

>>> from sage.all import *
>>> d.keys()   # random order
[0.500000000000000, 10, 3, 20]
>>> sorted(d.keys())
[0.500000000000000, 3, 10, 20]

Sage

sage: d.values()   # random order
[(1, 2, 3), 'newvalue', 14, 'newervalue']
sage: set(d.values()) == set([14, (1, 2, 3), 'newvalue', 'newervalue'])
True

Python

>>> from sage.all import *
>>> d.values()   # random order
[(1, 2, 3), 'newvalue', 14, 'newervalue']
>>> set(d.values()) == set([Integer(14), (Integer(1), Integer(2), Integer(3)), 'newvalue', 'newervalue'])
True

Sage

sage: d.items()    # random order
[(0.500000000000000, (1, 2, 3)), (10, 'newvalue'), (3, 14), (20, 'newervalue')]
sage: sorted([(key, value) for key, value in d.items()])
[(0.500000000000000, (1, 2, 3)), (3, 14), (10, 'newvalue'), (20, 'newervalue')]

Python

>>> from sage.all import *
>>> d.items()    # random order
[(0.500000000000000, (1, 2, 3)), (10, 'newvalue'), (3, 14), (20, 'newervalue')]
>>> sorted([(key, value) for key, value in d.items()])
[(0.500000000000000, (1, 2, 3)), (3, 14), (10, 'newvalue'), (20, 'newervalue')]

Exercise: Consider the following directed graph.

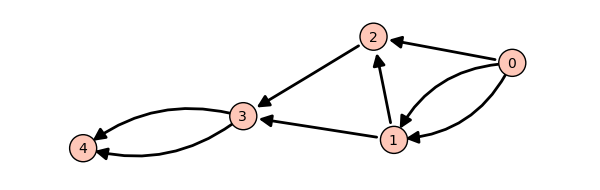
Create a dictionary whose keys are the vertices of the above directed graph, and whose values are the lists of the vertices that it points to. For instance, the vertex 1 points to the vertices 2 and 3, so the dictionary will look like:

d = { ..., 1:[2,3], ... }

Sage

sage: # edit here

Python

>>> from sage.all import *
>>> # edit here

Then try:

Sage

sage: g = DiGraph(d)
sage: g.plot()

Python

>>> from sage.all import *
>>> g = DiGraph(d)
>>> g.plot()

Using Sage types: The srange command#

Example: Construct a \(3 \times 3\) matrix whose \((i,j)\) entry is the rational number \(\frac{i}{j}\). The integers generated by range() are Python int’s. As a consequence, dividing them does euclidean division (in Python2):

Sage

sage: matrix([[i/j for j in range(1,4)] for i in range(1,4)]) # not tested
[1 0 0]
[2 1 0]
[3 1 1]

Python

>>> from sage.all import *
>>> matrix([[i/j for j in range(Integer(1),Integer(4))] for i in range(Integer(1),Integer(4))]) # not tested
[1 0 0]
[2 1 0]
[3 1 1]

In Python3, the division of Python integers returns a float instead.

Whereas dividing a Sage Integer by a Sage Integer produces a rational number:

Sage

sage: matrix([[ i/j for j in srange(1,4)] for i in srange(1,4)])
[  1 1/2 1/3]
[  2   1 2/3]
[  3 3/2   1]

Python

>>> from sage.all import *
>>> matrix([[ i/j for j in srange(Integer(1),Integer(4))] for i in srange(Integer(1),Integer(4))])
[  1 1/2 1/3]
[  2   1 2/3]
[  3 3/2   1]

Tutorial: Programming in Python and Sage#

Data structures#

Control structures#

Functions#

Exercises#

Lists#

Creating Lists I: [Square brackets]#

Creating Lists II: range#

Creating Lists III: list comprehensions#

Filtering lists with a list comprehension#

Nested list comprehensions#

Accessing individual elements of lists#

Modifying lists: changing an element in a list#

Modifying lists: append and extend#

Modifying lists: reverse, sort, …#

Concatenating Lists#

Slicing Lists#

Tuples#

Generators#

Dictionaries#

Using Sage types: The srange command#

Modifying lists has consequences!#

Loops and Functions#

While Loops#

For Loops#

Exercises#

Functions#

Exercises#