Finite lattices and semilattices¶

This module implements finite (semi)lattices. It defines:

`LatticePoset()`	Construct a lattice.
`MeetSemilattice()`	Construct a meet semi-lattice.
`JoinSemilattice()`	Construct a join semi-lattice.
`FiniteLatticePoset`	A class for finite lattices.
`FiniteMeetSemilattice`	A class for finite meet semilattices.
`FiniteJoinSemilattice`	A class for finite join semilattices.

List of (semi)lattice methods¶

Meet and join

`meet()`	Return the meet of given elements.
`join()`	Return the join of given elements.
`meet_matrix()`	Return the matrix of meets of all elements of the meet semi-lattice.
`join_matrix()`	Return the matrix of joins of all elements of the join semi-lattice.

Properties of the lattice

`is_distributive()`	Return `True` if the lattice is distributive.
`is_modular()`	Return `True` if the lattice is modular.
`is_lower_semimodular()`	Return `True` if all elements with common upper cover have a common lower cover.
`is_upper_semimodular()`	Return `True` if all elements with common lower cover have a common upper cover.
`is_semidistributive()`	Return `True` if the lattice is both join- and meet-semidistributive.
`is_join_semidistributive()`	Return `True` if the lattice is join-semidistributive.
`is_meet_semidistributive()`	Return `True` if the lattice is meet-semidistributive.
`is_join_distributive()`	Return `True` if the lattice is join-distributive.
`is_meet_distributive()`	Return `True` if the lattice is meet-distributive.
`is_atomic()`	Return `True` if every element of the lattice can be written as a join of atoms.
`is_coatomic()`	Return `True` if every element of the lattice can be written as a meet of coatoms.
`is_geometric()`	Return `True` if the lattice is atomic and upper semimodular.
`is_extremal()`	Return `True` if the lattice is extremal.
`is_complemented()`	Return `True` if every element of the lattice has at least one complement.
`is_sectionally_complemented()`	Return `True` if every interval from the bottom is complemented.
`is_cosectionally_complemented()`	Return `True` if every interval to the top is complemented.
`is_relatively_complemented()`	Return `True` if every interval of the lattice is complemented.
`is_pseudocomplemented()`	Return `True` if every element of the lattice has a (meet-)pseudocomplement.
`is_join_pseudocomplemented()`	Return `True` if every element of the lattice has a join-pseudocomplement.
`is_orthocomplemented()`	Return `True` if the lattice has an orthocomplementation.
`is_supersolvable()`	Return `True` if the lattice is supersolvable.
`is_planar()`	Return `True` if the lattice has an upward planar drawing.
`is_dismantlable()`	Return `True` if the lattice is dismantlable.
`is_interval_dismantlable()`	Return `True` if the lattice is interval dismantlable.
`is_sublattice_dismantlable()`	Return `True` if the lattice is sublattice dismantlable.
`is_stone()`	Return `True` if the lattice is a Stone lattice.
`is_trim()`	Return `True` if the lattice is a trim lattice.
`is_vertically_decomposable()`	Return `True` if the lattice is vertically decomposable.
`is_simple()`	Return `True` if the lattice has no nontrivial congruences.
`is_isoform()`	Return `True` if all congruences of the lattice consists of isoform blocks.
`is_uniform()`	Return `True` if all congruences of the lattice consists of equal-sized blocks.
`is_regular()`	Return `True` if all congruences of lattice are determined by any of the congruence blocks.
`is_subdirectly_reducible()`	Return `True` if the lattice is a sublattice of the product of smaller lattices.
`is_constructible_by_doublings()`	Return `True` if the lattice is constructible by doublings from the one-element lattice.
`breadth()`	Return the breadth of the lattice.

Specific elements

`atoms()`	Return elements covering the bottom element.
`coatoms()`	Return elements covered by the top element.
`double_irreducibles()`	Return double irreducible elements.
`join_primes()`	Return the join prime elements.
`meet_primes()`	Return the meet prime elements.
`complements()`	Return the list of complements of an element, or the dictionary of complements for all elements.
`pseudocomplement()`	Return the pseudocomplement of an element.
`is_modular_element()`	Return `True` if given element is modular in the lattice.
`is_left_modular_element()`	Return `True` if given element is left modular in the lattice.
`neutral_elements()`	Return neutral elements of the lattice.
`canonical_joinands()`	Return the canonical joinands of an element.
`canonical_meetands()`	Return the canonical meetands of an element.

Sublattices

`sublattice()`	Return sublattice generated by list of elements.
`submeetsemilattice()`	Return meet-subsemilattice generated by list of elements.
`subjoinsemilattice()`	Return join-subsemilattice generated by list of elements.
`is_sublattice()`	Return `True` if the lattice is a sublattice of given lattice.
`sublattices()`	Return all sublattices of the lattice.
`sublattices_lattice()`	Return the lattice of sublattices.
`isomorphic_sublattices_iterator()`	Return an iterator over the sublattices isomorphic to given lattice.
`maximal_sublattices()`	Return maximal sublattices of the lattice.
`frattini_sublattice()`	Return the intersection of maximal sublattices of the lattice.
`skeleton()`	Return the skeleton of the lattice.
`center()`	Return the sublattice of complemented neutral elements.
`vertical_decomposition()`	Return the vertical decomposition of the lattice.

Miscellaneous

`moebius_algebra()`	Return the Möbius algebra of the lattice.
`quantum_moebius_algebra()`	Return the quantum Möbius algebra of the lattice.
`vertical_composition()`	Return ordinal sum of lattices with top/bottom element unified.
`day_doubling()`	Return the lattice with Alan Day’s doubling construction of a subset.
`adjunct()`	Return the adjunct with other lattice.
`subdirect_decomposition()`	Return the subdirect decomposition of the lattice.
`congruence()`	Return the congruence generated by lists of elements.
`quotient()`	Return the quotient lattice by a congruence.
`congruences_lattice()`	Return the lattice of congruences.

class sage.combinat.posets.lattices.FiniteJoinSemilattice(hasse_diagram, elements, category, facade, key)[source]¶

Bases: FinitePoset

We assume that the argument passed to FiniteJoinSemilattice is the poset of a join-semilattice (i.e. a poset with least upper bound for each pair of elements).

Element[source]¶: alias of JoinSemilatticeElement

coatoms()[source]¶

Return the list of co-atoms of this (semi)lattice.

A co-atom of a lattice is an element covered by the top element.

EXAMPLES:

Sage

sage: L = posets.DivisorLattice(60)
sage: sorted(L.coatoms())
[12, 20, 30]

Python

>>> from sage.all import *
>>> L = posets.DivisorLattice(Integer(60))
>>> sorted(L.coatoms())
[12, 20, 30]

See also

Dual function: atoms()

join(x, y=None)[source]¶

Return the join of given elements in the lattice.

INPUT:

x, y – two elements of the (semi)lattice OR
x – list or tuple of elements

EXAMPLES:

Sage

sage: D = posets.DiamondPoset(5)
sage: D.join(1, 2)
4
sage: D.join(1, 1)
1
sage: D.join(1, 4)
4
sage: D.join(1, 0)
1

Python

>>> from sage.all import *
>>> D = posets.DiamondPoset(Integer(5))
>>> D.join(Integer(1), Integer(2))
4
>>> D.join(Integer(1), Integer(1))
1
>>> D.join(Integer(1), Integer(4))
4
>>> D.join(Integer(1), Integer(0))
1

Using list of elements as an argument. Join of empty list is the bottom element:

Sage

sage: B4=posets.BooleanLattice(4)
sage: B4.join([2,4,8])
14
sage: B4.join([])
0

Python

>>> from sage.all import *
>>> B4=posets.BooleanLattice(Integer(4))
>>> B4.join([Integer(2),Integer(4),Integer(8)])
14
>>> B4.join([])
0

For non-facade lattices operator + works for join:

Sage

sage: L = posets.PentagonPoset(facade=False)
sage: L(1)+L(2)
4

Python

>>> from sage.all import *
>>> L = posets.PentagonPoset(facade=False)
>>> L(Integer(1))+L(Integer(2))
4

See also

Dual function: meet()

join_matrix()[source]¶

Return a matrix whose (i,j) entry is k, where self.linear_extension()[k] is the join (least upper bound) of self.linear_extension()[i] and self.linear_extension()[j].

EXAMPLES:

Sage

sage: P = LatticePoset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]], facade = False)
sage: J = P.join_matrix(); J
[0 1 2 3 4 5 6 7]
[1 1 3 3 7 7 7 7]
[2 3 2 3 4 6 6 7]
[3 3 3 3 7 7 7 7]
[4 7 4 7 4 7 7 7]
[5 7 6 7 7 5 6 7]
[6 7 6 7 7 6 6 7]
[7 7 7 7 7 7 7 7]
sage: J[P(4).vertex,P(3).vertex] == P(7).vertex
True
sage: J[P(5).vertex,P(2).vertex] == P(5).vertex
True
sage: J[P(5).vertex,P(2).vertex] == P(2).vertex
False

Python

>>> from sage.all import *
>>> P = LatticePoset([[Integer(1),Integer(3),Integer(2)],[Integer(4)],[Integer(4),Integer(5),Integer(6)],[Integer(6)],[Integer(7)],[Integer(7)],[Integer(7)],[]], facade = False)
>>> J = P.join_matrix(); J
[0 1 2 3 4 5 6 7]
[1 1 3 3 7 7 7 7]
[2 3 2 3 4 6 6 7]
[3 3 3 3 7 7 7 7]
[4 7 4 7 4 7 7 7]
[5 7 6 7 7 5 6 7]
[6 7 6 7 7 6 6 7]
[7 7 7 7 7 7 7 7]
>>> J[P(Integer(4)).vertex,P(Integer(3)).vertex] == P(Integer(7)).vertex
True
>>> J[P(Integer(5)).vertex,P(Integer(2)).vertex] == P(Integer(5)).vertex
True
>>> J[P(Integer(5)).vertex,P(Integer(2)).vertex] == P(Integer(2)).vertex
False

class sage.combinat.posets.lattices.FiniteLatticePoset(hasse_diagram, elements, category, facade, key)[source]¶

Bases: FiniteMeetSemilattice, FiniteJoinSemilattice

We assume that the argument passed to FiniteLatticePoset is the poset of a lattice (i.e. a poset with greatest lower bound and least upper bound for each pair of elements).

Element[source]¶: alias of LatticePosetElement

adjunct(other, a, b)[source]¶

Return the adjunct of the lattice by other on the pair \((a, b)\).

It is assumed that \(a < b\) but \(b\) does not cover \(a\).

The adjunct of a lattice \(K\) to \(L\) with respect to pair \((a, b)\) of \(L\) is defined such that \(x < y\) if

\(x, y \in K\) and \(x < y\) in \(K\),
\(x, y \in L\) and \(x < y\) in \(L\),
\(x \in L\), \(y \in K\) and \(x \le a\) in \(L\), or
\(x \in K\), \(y \in L\) and \(b \le y\) in \(L\).

Informally this can be seen as attaching the lattice \(K\) to \(L\) as a new block between \(a\) and \(b\). Dismantlable lattices are exactly those that can be created from chains with this function.

Mathematically, it is only defined when \(L\) and \(K\) have no common element; here we force that by giving them different names in the resulting lattice.

EXAMPLES:

Sage

sage: Pnum = posets.PentagonPoset()
sage: Palp = Pnum.relabel(lambda x: chr(ord('a')+x))
sage: PP = Pnum.adjunct(Palp, 0, 3)
sage: PP.atoms()
[(0, 1), (0, 2), (1, 'a')]
sage: PP.coatoms()
[(0, 1), (0, 3)]

Python

>>> from sage.all import *
>>> Pnum = posets.PentagonPoset()
>>> Palp = Pnum.relabel(lambda x: chr(ord('a')+x))
>>> PP = Pnum.adjunct(Palp, Integer(0), Integer(3))
>>> PP.atoms()
[(0, 1), (0, 2), (1, 'a')]
>>> PP.coatoms()
[(0, 1), (0, 3)]

breadth(certificate=False)[source]¶

Return the breadth of the lattice.

The breadth of a lattice is the largest integer \(n\) such that any join of elements \(x_1, x_2, \ldots, x_{n+1}\) is join of a proper subset of \(x_i\).

This can be also characterized by subposets: a lattice of breadth at least \(n\) contains a subposet isomorphic to the Boolean lattice of \(2^n\) elements.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return the pair \((b, a)\) where \(b\) is the breadth and \(a\) is an antichain such that the join of \(a\) differs from the join of any proper subset of \(a\). If certificate=False return just the breadth.

EXAMPLES:

Sage

sage: D10 = posets.DiamondPoset(10)
sage: D10.breadth()
2

sage: B3 = posets.BooleanLattice(3)
sage: B3.breadth()
3
sage: B3.breadth(certificate=True)
(3, [1, 2, 4])

Python

>>> from sage.all import *
>>> D10 = posets.DiamondPoset(Integer(10))
>>> D10.breadth()
2

>>> B3 = posets.BooleanLattice(Integer(3))
>>> B3.breadth()
3
>>> B3.breadth(certificate=True)
(3, [1, 2, 4])

ALGORITHM:

For a lattice to have breadth at least \(n\), it must have an \(n\)-element antichain \(A\) with join \(j\). Element \(j\) must cover at least \(n\) elements. There must also be \(n-2\) levels of elements between \(A\) and \(j\). So we start by searching elements that could be our \(j\) and then just check possible antichains \(A\).

Note

Prior to version 8.1 this function returned just an antichain with certificate=True.

canonical_joinands(e)[source]¶

Return the canonical joinands of \(e\).

The canonical joinands of an element \(e\) in the lattice \(L\) is the subset \(S \subseteq L\) such that 1) the join of \(S\) is \(e\), and 2) if the join of some other subset \(S'\) of is also \(e\), then for every element \(s \in S\) there is an element \(s' \in S'\) such that \(s \le s'\).

Informally said this is the set of lowest possible elements with given join. It exists for every element if and only if the lattice is join-semidistributive. Canonical joinands are always join-irreducibles.

INPUT:

e – an element of the lattice

OUTPUT: canonical joinands as a list, if it exists; if not, None

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3], 2: [4, 5], 3: [5], 4: [6],
....:                   5: [7], 6: [7]})
sage: L.canonical_joinands(7)
[3, 4]

sage: L = LatticePoset({1: [2, 3], 2: [4, 5], 3: [6], 4: [6],
....: 5: [6]})
sage: L.canonical_joinands(6) is None
True

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5)], Integer(3): [Integer(5)], Integer(4): [Integer(6)],
...                   Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.canonical_joinands(Integer(7))
[3, 4]

>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5)], Integer(3): [Integer(6)], Integer(4): [Integer(6)],
... Integer(5): [Integer(6)]})
>>> L.canonical_joinands(Integer(6)) is None
True

See also

canonical_meetands()

canonical_meetands(e)[source]¶

Return the canonical meetands of \(e\).

The canonical meetands of an element \(e\) in the lattice \(L\) is the subset \(S \subseteq L\) such that 1) the meet of \(S\) is \(e\), and 2) if the meet of some other subset \(S'\) of is also \(e\), then for every element \(s \in S\) there is an element \(s' \in S'\) such that \(s \ge s'\).

Informally said this is the set of greatest possible elements with given meet. It exists for every element if and only if the lattice is meet-semidistributive. Canonical meetands are always meet-irreducibles.

INPUT:

e – an element of the lattice

OUTPUT: canonical meetands as a list, if it exists; if not, None

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3], 2: [4], 3: [5, 6], 4: [6],
....:                   5: [7], 6: [7]})
sage: L.canonical_meetands(1)
[5, 4]

sage: L = LatticePoset({1: [2, 3], 2: [4, 5], 3: [6], 4: [6],
....: 5: [6]})
sage: L.canonical_meetands(1) is None
True

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4)], Integer(3): [Integer(5), Integer(6)], Integer(4): [Integer(6)],
...                   Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.canonical_meetands(Integer(1))
[5, 4]

>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5)], Integer(3): [Integer(6)], Integer(4): [Integer(6)],
... Integer(5): [Integer(6)]})
>>> L.canonical_meetands(Integer(1)) is None
True

See also

canonical_joinands()

center()[source]¶

Return the center of the lattice.

An element of a lattice is central if it is neutral and has a complement. The subposet induced by central elements is a center of the lattice. Actually it is a Boolean lattice.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [6, 7], 3: [8, 9, 7],
....:                   4: [5, 6], 5: [8, 10], 6: [10], 7: [13, 11],
....:                   8: [13, 12], 9: [11, 12], 10: [13],
....:                   11: [14], 12: [14], 13: [14]})
sage: C = L.center(); C
Finite lattice containing 4 elements
sage: C.cover_relations()
[[1, 2], [1, 12], [2, 14], [12, 14]]

sage: L = posets.DivisorLattice(60)
sage: sorted(L.center().list())
[1, 3, 4, 5, 12, 15, 20, 60]

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(6), Integer(7)], Integer(3): [Integer(8), Integer(9), Integer(7)],
...                   Integer(4): [Integer(5), Integer(6)], Integer(5): [Integer(8), Integer(10)], Integer(6): [Integer(10)], Integer(7): [Integer(13), Integer(11)],
...                   Integer(8): [Integer(13), Integer(12)], Integer(9): [Integer(11), Integer(12)], Integer(10): [Integer(13)],
...                   Integer(11): [Integer(14)], Integer(12): [Integer(14)], Integer(13): [Integer(14)]})
>>> C = L.center(); C
Finite lattice containing 4 elements
>>> C.cover_relations()
[[1, 2], [1, 12], [2, 14], [12, 14]]

>>> L = posets.DivisorLattice(Integer(60))
>>> sorted(L.center().list())
[1, 3, 4, 5, 12, 15, 20, 60]

See also

neutral_elements(), complements()

complements(element=None)[source]¶

Return the list of complements of an element in the lattice, or the dictionary of complements for all elements.

Elements \(x\) and \(y\) are complements if their meet and join are respectively the bottom and the top element of the lattice.

INPUT:

element – an element of the lattice whose complement is returned. If None (default) then dictionary of complements for all elements having at least one complement is returned.

EXAMPLES:

Sage

sage: L = LatticePoset({0:['a','b','c'],'a':[1],'b':[1],'c':[1]})
sage: C = L.complements()

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(0):['a','b','c'],'a':[Integer(1)],'b':[Integer(1)],'c':[Integer(1)]})
>>> C = L.complements()

Let us check that ‘a’ and ‘b’ are complements of each other:

Sage

sage: 'a' in C['b']
True
sage: 'b' in C['a']
True

Python

>>> from sage.all import *
>>> 'a' in C['b']
True
>>> 'b' in C['a']
True

Full list of complements:

Sage

sage: L.complements() # random order
{0: [1], 1: [0], 'a': ['b', 'c'], 'b': ['c', 'a'], 'c': ['b', 'a']}

sage: L = LatticePoset({0:[1,2],1:[3],2:[3],3:[4]})
sage: L.complements() # random order
{0: [4], 4: [0]}
sage: L.complements(1)
[]

Python

>>> from sage.all import *
>>> L.complements() # random order
{0: [1], 1: [0], 'a': ['b', 'c'], 'b': ['c', 'a'], 'c': ['b', 'a']}

>>> L = LatticePoset({Integer(0):[Integer(1),Integer(2)],Integer(1):[Integer(3)],Integer(2):[Integer(3)],Integer(3):[Integer(4)]})
>>> L.complements() # random order
{0: [4], 4: [0]}
>>> L.complements(Integer(1))
[]

See also

is_complemented()

congruence(S)[source]¶

Return the congruence generated by set of sets \(S\).

A congruence of a lattice is an equivalence relation \(\cong\) that is compatible with meet and join; i.e. if \(a_1 \cong a_2\) and \(b_1 \cong b_2\), then \((a_1 \\vee b_1) \cong (a_2 \\vee b_2)\) and \((a_1 \wedge b_1) \cong (a_2 \wedge b_2)\).

By the congruence generated by set of sets \(\{S_1, \ldots, S_n\}\) we mean the least congruence \(\cong\) such that for every \(x, y \in S_i\) for some \(i\) we have \(x \cong y\).

INPUT:

S – list of lists; list of element blocks that the congruence will contain

OUTPUT:

Congruence of the lattice as a sage.combinat.set_partition.SetPartition.

EXAMPLES:

Sage

sage: # needs sage.combinat
sage: L = posets.DivisorLattice(12)
sage: cong = L.congruence([[1, 3]])
sage: sorted(sorted(c) for c in cong)
[[1, 3], [2, 6], [4, 12]]
sage: L.congruence([[1, 2], [6, 12]])
{{1, 2, 4}, {3, 6, 12}}

sage: L = LatticePoset({1: [2, 3], 2: [4], 3: [4], 4: [5]})
sage: L.congruence([[1, 2]])                                                # needs sage.combinat
{{1, 2}, {3, 4}, {5}}

sage: L = LatticePoset({1: [2, 3], 2: [4, 5, 6], 4: [5], 5: [7, 8],
....:                   6: [8], 3: [9], 7: [10], 8: [10], 9:[10]})
sage: cong = L.congruence([[1, 2]])                                         # needs sage.combinat
sage: cong[0]                                                               # needs sage.combinat
frozenset({1, 2, 3, 4, 5, 6, 7, 8, 9, 10})

Python

>>> from sage.all import *
>>> # needs sage.combinat
>>> L = posets.DivisorLattice(Integer(12))
>>> cong = L.congruence([[Integer(1), Integer(3)]])
>>> sorted(sorted(c) for c in cong)
[[1, 3], [2, 6], [4, 12]]
>>> L.congruence([[Integer(1), Integer(2)], [Integer(6), Integer(12)]])
{{1, 2, 4}, {3, 6, 12}}

>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4)], Integer(3): [Integer(4)], Integer(4): [Integer(5)]})
>>> L.congruence([[Integer(1), Integer(2)]])                                                # needs sage.combinat
{{1, 2}, {3, 4}, {5}}

>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5), Integer(6)], Integer(4): [Integer(5)], Integer(5): [Integer(7), Integer(8)],
...                   Integer(6): [Integer(8)], Integer(3): [Integer(9)], Integer(7): [Integer(10)], Integer(8): [Integer(10)], Integer(9):[Integer(10)]})
>>> cong = L.congruence([[Integer(1), Integer(2)]])                                         # needs sage.combinat
>>> cong[Integer(0)]                                                               # needs sage.combinat
frozenset({1, 2, 3, 4, 5, 6, 7, 8, 9, 10})

See also

quotient()

congruences_lattice(labels='congruence')[source]¶

Return the lattice of congruences.

A congruence of a lattice is a partition of elements to classes compatible with both meet- and join-operation; see congruence(). Elements of the congruence lattice are congruences ordered by refinement; i.e. if every class of a congruence \(\Theta\) is contained in some class of \(\Phi\), then \(\Theta \le \Phi\) in the congruence lattice.

INPUT:

labels – string; the type of elements in the resulting lattice

OUTPUT: a distributive lattice

If labels='congruence', then elements of the result will be congruences given as sage.combinat.set_partition.SetPartition.
If labels='integers', result is a lattice on integers isomorphic to the congruence lattice.

EXAMPLES:

Sage

sage: # needs sage.combinat
sage: N5 = posets.PentagonPoset()
sage: CL = N5.congruences_lattice(); CL
Finite lattice containing 5 elements
sage: CL.atoms()
[{{0}, {1}, {2, 3}, {4}}]
sage: CL.coatoms()
[{{0, 1}, {2, 3, 4}}, {{0, 2, 3}, {1, 4}}]

sage: C4 = posets.ChainPoset(4)
sage: CL = C4.congruences_lattice(labels='integer')                         # needs sage.combinat
sage: CL.is_isomorphic(posets.BooleanLattice(3))                            # needs sage.combinat
True

Python

>>> from sage.all import *
>>> # needs sage.combinat
>>> N5 = posets.PentagonPoset()
>>> CL = N5.congruences_lattice(); CL
Finite lattice containing 5 elements
>>> CL.atoms()
[{{0}, {1}, {2, 3}, {4}}]
>>> CL.coatoms()
[{{0, 1}, {2, 3, 4}}, {{0, 2, 3}, {1, 4}}]

>>> C4 = posets.ChainPoset(Integer(4))
>>> CL = C4.congruences_lattice(labels='integer')                         # needs sage.combinat
>>> CL.is_isomorphic(posets.BooleanLattice(Integer(3)))                            # needs sage.combinat
True

day_doubling(S)[source]¶

Return the lattice with Alan Day’s doubling construction of subset \(S\).

The subset \(S\) is assumed to be convex (i.e. if \(a, c \in S\) and \(a < b < c\) in the lattice, then \(b \in S\)) and connected (i.e. if \(a, b \in S\) then there is a chain \(a=e_1, e_2, \ldots, e_n=b\) such that \(e_i\) either covers or is covered by \(e_{i+1}\)).

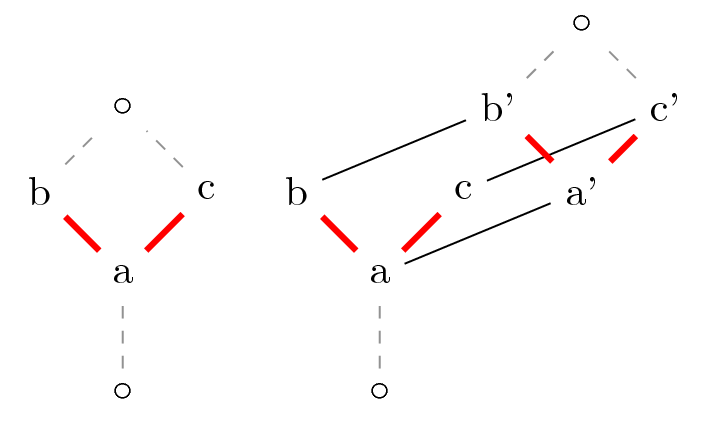
Alan Day’s doubling construction is a specific extension of the lattice. Here we formulate it in a format more suitable for computation.

Let \(L\) be a lattice and \(S\) a convex subset of it. The resulting lattice \(L[S]\) has elements \((e, 0)\) for each \(e \in L\) and \((e, 1)\) for each \(e \in S\). If \(x \le y\) in \(L\), then in the new lattice we have

\((x, 0), (x, 1) \le (y, 0), (y, 1)\)
\((x, 0) \le (x, 1)\)

INPUT:

S – a subset of the lattice

EXAMPLES:

Sage

sage: L = LatticePoset({1: ['a', 'b', 2], 'a': ['c'], 'b': ['c', 'd'],
....:                   2: [3], 'c': [4], 'd': [4], 3: [4]})
sage: L2 = L.day_doubling(['a', 'b', 'c', 'd']); L2
Finite lattice containing 12 elements
sage: set(L2.upper_covers((1, 0))) == set([(2, 0), ('a', 0), ('b', 0)])
True
sage: set(L2.upper_covers(('b', 0))) == set([('d', 0), ('b', 1), ('c', 0)])
True

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): ['a', 'b', Integer(2)], 'a': ['c'], 'b': ['c', 'd'],
...                   Integer(2): [Integer(3)], 'c': [Integer(4)], 'd': [Integer(4)], Integer(3): [Integer(4)]})
>>> L2 = L.day_doubling(['a', 'b', 'c', 'd']); L2
Finite lattice containing 12 elements
>>> set(L2.upper_covers((Integer(1), Integer(0)))) == set([(Integer(2), Integer(0)), ('a', Integer(0)), ('b', Integer(0))])
True
>>> set(L2.upper_covers(('b', Integer(0)))) == set([('d', Integer(0)), ('b', Integer(1)), ('c', Integer(0))])
True

See also

is_constructible_by_doublings()

double_irreducibles()[source]¶

Return the list of double irreducible elements of this lattice.

A double irreducible element of a lattice is an element covering and covered by exactly one element. In other words it is neither a meet nor a join of any elements.

EXAMPLES:

Sage

sage: L = posets.DivisorLattice(12)
sage: sorted(L.double_irreducibles())
[3, 4]

sage: L = posets.BooleanLattice(3)
sage: L.double_irreducibles()
[]

Python

>>> from sage.all import *
>>> L = posets.DivisorLattice(Integer(12))
>>> sorted(L.double_irreducibles())
[3, 4]

>>> L = posets.BooleanLattice(Integer(3))
>>> L.double_irreducibles()
[]

feichtner_yuzvinsky_ring(G, use_defining=False, base_ring=None)[source]¶

Return the Feichtner-Yuzvinsky ring of self and G.

Let \(R\) be a commutative ring, \(L\) a lattice, and \(G \subseteq L\). The Feichtner-Yuzvinsky ring is the quotient of the polynomial ring \(R[h_g \mid g \in G]\) by the ideal generated by

\(h_a\) for every atom \(a \in L \cap G\) and
for every antichain \(A\) of the subposet \(G\) such that \(g := \bigvee A \in G\) (with the join taken in \(L\))

\[\prod_{a \in A} (h_g - h_a).\]

This was originally described for \(G\) such that \((L, G)\) is a built lattice in the sense of [FY2004] (which has a geometric motivation), but this has been extended to \(G\) being an arbitrary subset.

This is not the original definition, which uses the nested subsets of \(G\) (see [FY2004] for the definition). However, the original construction, which we call the defining presentation and use the variables \(\{x_g \mid g \in G\}\), can be recovered by setting \(h_g = \sum_{g' \geq g} x_{g'}\) (where \(g' \in G\)).

INPUT:

G – a subset of elements of self
use_defining – boolean (default: False); whether or not to use the defining presentation in \(x_g\)
base_ring – (default: \(\QQ\)) the base ring

The order on the variables is equal to the ordering of the elements in G.

EXAMPLES:

Sage

sage: B2 = posets.BooleanLattice(2)
sage: FY = B2.feichtner_yuzvinsky_ring(B2[1:])
sage: FY
Quotient of Multivariate Polynomial Ring in h0, h1, h2 over Rational Field
 by the ideal (h0, h1, h0*h1 - h0*h2 - h1*h2 + h2^2)

sage: FY = B2.feichtner_yuzvinsky_ring(B2[1:], use_defining=True)
sage: FY
Quotient of Multivariate Polynomial Ring in x0, x1, x2 over Rational Field
 by the ideal (x0 + x2, x1 + x2, x0*x1)

Python

>>> from sage.all import *
>>> B2 = posets.BooleanLattice(Integer(2))
>>> FY = B2.feichtner_yuzvinsky_ring(B2[Integer(1):])
>>> FY
Quotient of Multivariate Polynomial Ring in h0, h1, h2 over Rational Field
 by the ideal (h0, h1, h0*h1 - h0*h2 - h1*h2 + h2^2)

>>> FY = B2.feichtner_yuzvinsky_ring(B2[Integer(1):], use_defining=True)
>>> FY
Quotient of Multivariate Polynomial Ring in x0, x1, x2 over Rational Field
 by the ideal (x0 + x2, x1 + x2, x0*x1)

We reproduce the example from Section 5 of [Coron2023]:

Sage

sage: # needs sage.geometry.polyhedron
sage: H.<a,b,c,d> = HyperplaneArrangements(QQ)
sage: Arr = H(a-b, b-c, c-d, d-a)
sage: P = LatticePoset(Arr.intersection_poset())
sage: FY = P.feichtner_yuzvinsky_ring([P.top(),5,1,2,3,4])
sage: FY.defining_ideal().groebner_basis()                                  # needs sage.libs.singular
[h0^2 - h0*h1, h1^2, h2, h3, h4, h5]

Python

>>> from sage.all import *
>>> # needs sage.geometry.polyhedron
>>> H = HyperplaneArrangements(QQ, names=('a', 'b', 'c', 'd',)); (a, b, c, d,) = H._first_ngens(4)
>>> Arr = H(a-b, b-c, c-d, d-a)
>>> P = LatticePoset(Arr.intersection_poset())
>>> FY = P.feichtner_yuzvinsky_ring([P.top(),Integer(5),Integer(1),Integer(2),Integer(3),Integer(4)])
>>> FY.defining_ideal().groebner_basis()                                  # needs sage.libs.singular
[h0^2 - h0*h1, h1^2, h2, h3, h4, h5]

frattini_sublattice()[source]¶

Return the Frattini sublattice of the lattice.

The Frattini sublattice \(\Phi(L)\) is the intersection of all proper maximal sublattices of \(L\). It is also the set of “non-generators” - if the sublattice generated by set \(S\) of elements is whole lattice, then also \(S \setminus \Phi(L)\) generates whole lattice.

EXAMPLES:

Sage

sage: L = LatticePoset(( [], [[1,2],[1,17],[1,8],[2,3],[2,22],
....:                         [2,5],[2,7],[17,22],[17,13],[8,7],
....:                         [8,13],[3,16],[3,9],[22,16],[22,18],
....:                         [22,10],[5,18],[5,14],[7,9],[7,14],
....:                         [7,10],[13,10],[16,6],[16,19],[9,19],
....:                         [18,6],[18,33],[14,33],[10,19],
....:                         [10,33],[6,4],[19,4],[33,4]] ))
sage: sorted(L.frattini_sublattice().list())
[1, 2, 4, 10, 19, 22, 33]

Python

>>> from sage.all import *
>>> L = LatticePoset(( [], [[Integer(1),Integer(2)],[Integer(1),Integer(17)],[Integer(1),Integer(8)],[Integer(2),Integer(3)],[Integer(2),Integer(22)],
...                         [Integer(2),Integer(5)],[Integer(2),Integer(7)],[Integer(17),Integer(22)],[Integer(17),Integer(13)],[Integer(8),Integer(7)],
...                         [Integer(8),Integer(13)],[Integer(3),Integer(16)],[Integer(3),Integer(9)],[Integer(22),Integer(16)],[Integer(22),Integer(18)],
...                         [Integer(22),Integer(10)],[Integer(5),Integer(18)],[Integer(5),Integer(14)],[Integer(7),Integer(9)],[Integer(7),Integer(14)],
...                         [Integer(7),Integer(10)],[Integer(13),Integer(10)],[Integer(16),Integer(6)],[Integer(16),Integer(19)],[Integer(9),Integer(19)],
...                         [Integer(18),Integer(6)],[Integer(18),Integer(33)],[Integer(14),Integer(33)],[Integer(10),Integer(19)],
...                         [Integer(10),Integer(33)],[Integer(6),Integer(4)],[Integer(19),Integer(4)],[Integer(33),Integer(4)]] ))
>>> sorted(L.frattini_sublattice().list())
[1, 2, 4, 10, 19, 22, 33]

is_atomic(certificate=False)[source]¶

Return True if the lattice is atomic, and False otherwise.

A lattice is atomic if every element can be written as a join of atoms.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, e), where \(e\) is a join-irreducible element that is not an atom. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [5], 3:[5], 4:[6], 5:[6]})
sage: L.is_atomic()
True

sage: L = LatticePoset({0: [1, 2], 1: [3], 2: [3], 3:[4]})
sage: L.is_atomic()
False
sage: L.is_atomic(certificate=True)
(False, 4)

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5)], Integer(3):[Integer(5)], Integer(4):[Integer(6)], Integer(5):[Integer(6)]})
>>> L.is_atomic()
True

>>> L = LatticePoset({Integer(0): [Integer(1), Integer(2)], Integer(1): [Integer(3)], Integer(2): [Integer(3)], Integer(3):[Integer(4)]})
>>> L.is_atomic()
False
>>> L.is_atomic(certificate=True)
(False, 4)

Note

See [EnumComb1], Section 3.3 for a discussion of atomic lattices.

See also

Dual property: is_coatomic()
Stronger properties: is_sectionally_complemented()
Mutually exclusive properties: is_vertically_decomposable()

is_coatomic(certificate=False)[source]¶

Return True if the lattice is coatomic, and False otherwise.

A lattice is coatomic if every element can be written as a meet of coatoms; i.e. if the dual of the lattice is atomic.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, e), where \(e\) is a meet-irreducible element that is not a coatom. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = posets.BooleanLattice(3)
sage: L.is_coatomic()
True

sage: L = LatticePoset({1: [2], 2: [3, 4], 3: [5], 4:[5]})
sage: L.is_coatomic()
False
sage: L.is_coatomic(certificate=True)
(False, 1)

Python

>>> from sage.all import *
>>> L = posets.BooleanLattice(Integer(3))
>>> L.is_coatomic()
True

>>> L = LatticePoset({Integer(1): [Integer(2)], Integer(2): [Integer(3), Integer(4)], Integer(3): [Integer(5)], Integer(4):[Integer(5)]})
>>> L.is_coatomic()
False
>>> L.is_coatomic(certificate=True)
(False, 1)

See also

Dual property: is_atomic()
Stronger properties: is_cosectionally_complemented()
Mutually exclusive properties: is_vertically_decomposable()

is_complemented(certificate=False)[source]¶

Return True if the lattice is complemented, and False otherwise.

A lattice is complemented if every element has at least one complement.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, e), where e is an element without a complement. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({0: [1, 2, 3], 1: [4], 2: [4], 3: [4]})
sage: L.is_complemented()
True

sage: L = LatticePoset({1: [2, 3, 4], 2: [5, 6], 3: [5], 4: [6],
....:                   5: [7], 6: [7]})
sage: L.is_complemented()
False
sage: L.is_complemented(certificate=True)
(False, 2)

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(0): [Integer(1), Integer(2), Integer(3)], Integer(1): [Integer(4)], Integer(2): [Integer(4)], Integer(3): [Integer(4)]})
>>> L.is_complemented()
True

>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5), Integer(6)], Integer(3): [Integer(5)], Integer(4): [Integer(6)],
...                   Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.is_complemented()
False
>>> L.is_complemented(certificate=True)
(False, 2)

See also

Stronger properties: is_sectionally_complemented(), is_cosectionally_complemented(), is_orthocomplemented()
Other: complements()

is_constructible_by_doublings(type)[source]¶

Return True if the lattice is constructible by doublings, and False otherwise.

We call a lattice doubling constructible if it can be constructed from the one element lattice by a sequence of Alan Day’s doubling constructions.

Lattices constructible by interval doubling are also called bounded. Lattices constructible by lower and upper pseudo-interval are called lower bounded and upper bounded. Lattices constructible by any convex set doubling are called congruence normal.

INPUT:

type – string; can be one of the following:
- 'interval' – allow only doublings of an interval
- 'lower' – allow doublings of lower pseudo-interval; that is, a subset of the lattice with a unique minimal element
- 'upper' – allow doublings of upper pseudo-interval; that is, a subset of the lattice with a unique maximal element
- 'convex' – allow doubling of any convex set
- 'any' – allow doubling of any set

EXAMPLES:

The pentagon can be constructed by doubling intervals; the 5-element diamond can not be constructed by any doublings:

Sage

sage: posets.PentagonPoset().is_constructible_by_doublings('interval')
True

sage: posets.DiamondPoset(5).is_constructible_by_doublings('any')           # needs sage.combinat
False

Python

>>> from sage.all import *
>>> posets.PentagonPoset().is_constructible_by_doublings('interval')
True

>>> posets.DiamondPoset(Integer(5)).is_constructible_by_doublings('any')           # needs sage.combinat
False

After doubling both upper and lower pseudo-interval a lattice is constructible by convex subset doubling:

Sage

sage: L = posets.BooleanLattice(2)
sage: L = L.day_doubling([0, 1, 2])  # A lower pseudo-interval
sage: L.is_constructible_by_doublings('interval')
False
sage: L.is_constructible_by_doublings('lower')
True
sage: L = L.day_doubling([(3,0), (1,1), (2,1)])  # An upper pseudo-interval
sage: L.is_constructible_by_doublings('upper')
False
sage: L.is_constructible_by_doublings('convex')                             # needs sage.combinat
True

Python

>>> from sage.all import *
>>> L = posets.BooleanLattice(Integer(2))
>>> L = L.day_doubling([Integer(0), Integer(1), Integer(2)])  # A lower pseudo-interval
>>> L.is_constructible_by_doublings('interval')
False
>>> L.is_constructible_by_doublings('lower')
True
>>> L = L.day_doubling([(Integer(3),Integer(0)), (Integer(1),Integer(1)), (Integer(2),Integer(1))])  # An upper pseudo-interval
>>> L.is_constructible_by_doublings('upper')
False
>>> L.is_constructible_by_doublings('convex')                             # needs sage.combinat
True

An example of a lattice that can be constructed by doublings of a non-convex subsets:

Sage

sage: L = LatticePoset(DiGraph('OQC?a?@CO?G_C@?GA?O??_??@?BO?A_?G??C??_?@???'))
sage: L.is_constructible_by_doublings('convex')
False
sage: L.is_constructible_by_doublings('any')
True

Python

>>> from sage.all import *
>>> L = LatticePoset(DiGraph('OQC?a?@CO?G_C@?GA?O??_??@?BO?A_?G??C??_?@???'))
>>> L.is_constructible_by_doublings('convex')
False
>>> L.is_constructible_by_doublings('any')
True

See also

Stronger properties: is_distributive() (doubling by interval), is_join_semidistributive() (doubling by lower pseudo-intervals), is_meet_semidistributive() (doubling by upper pseudo-intervals)
Mutually exclusive properties: is_simple() (doubling by any set)
Other: day_doubling()

ALGORITHM:

According to [HOLM2016] a lattice \(L\) is lower bounded if and only if \(|\mathrm{Ji}(L)| = |\mathrm{Ji}(\mathrm{Con}\ L)|\), and so dually \(|\mathrm{Mi}(L)| = |\mathrm{Mi}(\mathrm{Con}\ L)|\) in upper bounded lattices. The same reference gives a test for being constructible by convex or by any subset.

is_cosectionally_complemented(certificate=False)[source]¶

Return True if the lattice is cosectionally complemented, and False otherwise.

A lattice is cosectionally complemented if all intervals to the top element interpreted as sublattices are complemented lattices.

INPUT:

certificate – boolean (default: False); whether to return a certificate if the lattice is not cosectionally complemented

OUTPUT:

If certificate=False return True or False. If certificate=True return either (True, None) or (False, (b, e)), where \(b\) is an element so that in the sublattice from \(b\) to the top element has no complement for element \(e\).

EXAMPLES:

The smallest sectionally but not cosectionally complemented lattice:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [5], 3: [5], 4: [6], 5: [6]})
sage: L.is_sectionally_complemented(), L.is_cosectionally_complemented()
(True, False)

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5)], Integer(3): [Integer(5)], Integer(4): [Integer(6)], Integer(5): [Integer(6)]})
>>> L.is_sectionally_complemented(), L.is_cosectionally_complemented()
(True, False)

A sectionally and cosectionally but not relatively complemented lattice:

Sage

sage: L = LatticePoset(DiGraph('MYi@O?P??D?OG?@?O_?C?Q??O?W?@??O??'))
sage: L.is_sectionally_complemented() and L.is_cosectionally_complemented()
True
sage: L.is_relatively_complemented()
False

Python

>>> from sage.all import *
>>> L = LatticePoset(DiGraph('MYi@O?P??D?OG?@?O_?C?Q??O?W?@??O??'))
>>> L.is_sectionally_complemented() and L.is_cosectionally_complemented()
True
>>> L.is_relatively_complemented()
False

Getting a certificate:

Sage

sage: L = LatticePoset(DiGraph('HW?@D?Q?GE?G@??'))
sage: L.is_cosectionally_complemented(certificate=True)
(False, (2, 7))

Python

>>> from sage.all import *
>>> L = LatticePoset(DiGraph('HW?@D?Q?GE?G@??'))
>>> L.is_cosectionally_complemented(certificate=True)
(False, (2, 7))

See also

Dual property: is_sectionally_complemented()
Weaker properties: is_complemented(), is_coatomic(), is_regular()
Stronger properties: is_relatively_complemented()

is_dismantlable(certificate=False)[source]¶

Return True if the lattice is dismantlable, and False otherwise.

An \(n\)-element lattice \(L_n\) is dismantlable if there is a sublattice chain \(L_{n-1} \supset L_{n-2}, \supset \cdots, \supset L_0\) so that every \(L_i\) is a sublattice of \(L_{i+1}\) with one element less, and \(L_0\) is the empty lattice. In other words, a dismantlable lattice can be reduced to empty lattice removing doubly irreducible element one by one.

INPUT:

certificate – boolean; whether to return a certificate
- If certificate = False (default), returns True or False accordingly.
- If certificate = True, returns:
  - (True, elms) when the lattice is dismantlable, where elms is elements listed in a possible removing order.
  - (False, crown) when the lattice is not dismantlable, where crown is a subposet of \(2k\) elements \(a_1, \ldots, a_k, b_1, \ldots, b_k\) with covering relations \(a_i \lessdot b_i\) and \(a_i \lessdot b_{i+1}\) for \(i \in [1, \ldots, k-1]\), and \(a_k \lessdot b_1\).

EXAMPLES:

Sage

sage: DL12 = LatticePoset((divisors(12), attrcall("divides")))
sage: DL12.is_dismantlable()
True
sage: DL12.is_dismantlable(certificate=True)
(True, [4, 2, 1, 3, 6, 12])

sage: B3 = posets.BooleanLattice(3)
sage: B3.is_dismantlable()
False
sage: B3.is_dismantlable(certificate=True)
(False, Finite poset containing 6 elements)

Python

>>> from sage.all import *
>>> DL12 = LatticePoset((divisors(Integer(12)), attrcall("divides")))
>>> DL12.is_dismantlable()
True
>>> DL12.is_dismantlable(certificate=True)
(True, [4, 2, 1, 3, 6, 12])

>>> B3 = posets.BooleanLattice(Integer(3))
>>> B3.is_dismantlable()
False
>>> B3.is_dismantlable(certificate=True)
(False, Finite poset containing 6 elements)

Every planar lattice is dismantlable. Converse is not true:

Sage

sage: L = LatticePoset( ([], [[0, 1], [0, 2], [0, 3], [0, 4],
....:                         [1, 7], [2, 6], [3, 5], [4, 5],
....:                         [4, 6], [4, 7], [5, 8], [6, 8],
....:                         [7, 8]]) )
sage: L.is_dismantlable()
True
sage: L.is_planar()
False

Python

>>> from sage.all import *
>>> L = LatticePoset( ([], [[Integer(0), Integer(1)], [Integer(0), Integer(2)], [Integer(0), Integer(3)], [Integer(0), Integer(4)],
...                         [Integer(1), Integer(7)], [Integer(2), Integer(6)], [Integer(3), Integer(5)], [Integer(4), Integer(5)],
...                         [Integer(4), Integer(6)], [Integer(4), Integer(7)], [Integer(5), Integer(8)], [Integer(6), Integer(8)],
...                         [Integer(7), Integer(8)]]) )
>>> L.is_dismantlable()
True
>>> L.is_planar()
False

See also

Stronger properties: is_planar()
Weaker properties: is_sublattice_dismantlable()

is_distributive(certificate=False)[source]¶

Return True if the lattice is distributive, and False otherwise.

A lattice \((L, \vee, \wedge)\) is distributive if meet distributes over join: \(x \wedge (y \vee z) = (x \wedge y) \vee (x \wedge z)\) for every \(x,y,z \in L\) just like \(x \cdot (y+z)=x \cdot y + x \cdot z\) in normal arithmetic. For duality in lattices it follows that then also join distributes over meet.

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, (x, y, z)), where \(x\), \(y\) and \(z\) are elements of the lattice such that \(x \wedge (y \vee z) \neq (x \wedge y) \vee (x \wedge z)\). If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3], 2: [4], 3: [4], 4: [5]})
sage: L.is_distributive()
True
sage: L = LatticePoset({1: [2, 3, 4], 2: [5], 3: [6], 4: [6], 5: [6]})
sage: L.is_distributive()
False
sage: L.is_distributive(certificate=True)
(False, (5, 3, 2))

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4)], Integer(3): [Integer(4)], Integer(4): [Integer(5)]})
>>> L.is_distributive()
True
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5)], Integer(3): [Integer(6)], Integer(4): [Integer(6)], Integer(5): [Integer(6)]})
>>> L.is_distributive()
False
>>> L.is_distributive(certificate=True)
(False, (5, 3, 2))

See also

Weaker properties: is_modular(), is_semidistributive(), is_join_distributive(), is_meet_distributive(), is_subdirectly_reducible(), is_trim(), is_constructible_by_doublings() (by interval doubling), is_extremal()
Stronger properties: is_stone()

is_extremal()[source]¶

Return True if the lattice is extremal, and False otherwise.

A lattice is extremal if the number of join-irreducibles is equal to the number of meet-irreducibles and to the number of cover relations in the longest chains.

EXAMPLES:

Sage

sage: posets.PentagonPoset().is_extremal()
True

sage: P = LatticePoset(posets.SymmetricGroupWeakOrderPoset(3))
sage: P.is_extremal()
False

Python

>>> from sage.all import *
>>> posets.PentagonPoset().is_extremal()
True

>>> P = LatticePoset(posets.SymmetricGroupWeakOrderPoset(Integer(3)))
>>> P.is_extremal()
False

See also

Stronger properties: is_distributive(), is_trim()

REFERENCES:

[Mark1992]

is_geometric()[source]¶

Return True if the lattice is geometric, and False otherwise.

A lattice is geometric if it is both atomic and upper semimodular.

EXAMPLES:

Canonical example is the lattice of partitions of finite set ordered by refinement:

Sage

sage: L = posets.SetPartitions(4)                                           # needs sage.combinat
sage: L.is_geometric()                                                      # needs sage.combinat
True

Python

>>> from sage.all import *
>>> L = posets.SetPartitions(Integer(4))                                           # needs sage.combinat
>>> L.is_geometric()                                                      # needs sage.combinat
True

Smallest example of geometric lattice that is not modular:

Sage

sage: L = LatticePoset(DiGraph('K]?@g@S?q?M?@?@?@?@?@?@??'))
sage: L.is_geometric()
True
sage: L.is_modular()
False

Python

>>> from sage.all import *
>>> L = LatticePoset(DiGraph('K]?@g@S?q?M?@?@?@?@?@?@??'))
>>> L.is_geometric()
True
>>> L.is_modular()
False

Two non-examples:

Sage

sage: L = LatticePoset({1:[2, 3, 4], 2:[5, 6], 3:[5], 4:[6], 5:[7], 6:[7]})
sage: L.is_geometric()  # Graded, but not upper semimodular
False
sage: L = posets.ChainPoset(3)
sage: L.is_geometric()  # Modular, but not atomic
False

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1):[Integer(2), Integer(3), Integer(4)], Integer(2):[Integer(5), Integer(6)], Integer(3):[Integer(5)], Integer(4):[Integer(6)], Integer(5):[Integer(7)], Integer(6):[Integer(7)]})
>>> L.is_geometric()  # Graded, but not upper semimodular
False
>>> L = posets.ChainPoset(Integer(3))
>>> L.is_geometric()  # Modular, but not atomic
False

See also

Weaker properties: is_upper_semimodular(), is_relatively_complemented()

is_interval_dismantlable(certificate=False)[source]¶

Return True if the lattice is interval dismantlable, and False otherwise.

An interval dismantling is a subdivision of a lattice to a principal upper set and a principal lower set. A lattice is interval dismantlable if it can be decomposed into 1-element lattices by consecutive interval distmantlings.

A lattice is minimally interval non-dismantlable if it is not interval dismantlable, but all of its sublattices are interval dismantlable.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

if certificate=False, return only True or False
if certificate=True, return either
- (True, list) where list is a nested list showing the decomposition; for example list[1][0] is a lower part of upper part of the lattice when decomposed twice.
- (False, M) where \(M\) is a minimally interval non-dismantlable sublattice of the lattice.

EXAMPLES:

Sage

sage: L1 = LatticePoset({1: [2, 3], 3: [4, 5], 2: [6], 4: [6], 5: [6]})
sage: L1.is_interval_dismantlable()
True

sage: L2 = LatticePoset({1: [2, 3, 4, 5], 2: [6], 3: [6], 4: [6],
....:                    5: [6, 7], 6: [8], 7: [9, 10], 8:[10], 9:[10]})
sage: L2.is_interval_dismantlable()
False

Python

>>> from sage.all import *
>>> L1 = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(3): [Integer(4), Integer(5)], Integer(2): [Integer(6)], Integer(4): [Integer(6)], Integer(5): [Integer(6)]})
>>> L1.is_interval_dismantlable()
True

>>> L2 = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4), Integer(5)], Integer(2): [Integer(6)], Integer(3): [Integer(6)], Integer(4): [Integer(6)],
...                    Integer(5): [Integer(6), Integer(7)], Integer(6): [Integer(8)], Integer(7): [Integer(9), Integer(10)], Integer(8):[Integer(10)], Integer(9):[Integer(10)]})
>>> L2.is_interval_dismantlable()
False

To get certificates:

Sage

sage: L1.is_interval_dismantlable(certificate=True)
(True, [[[1], [2]], [[[3], [5]], [[4], [6]]]])
sage: L2.is_interval_dismantlable(certificate=True)
(False, Finite lattice containing 5 elements)

Python

>>> from sage.all import *
>>> L1.is_interval_dismantlable(certificate=True)
(True, [[[1], [2]], [[[3], [5]], [[4], [6]]]])
>>> L2.is_interval_dismantlable(certificate=True)
(False, Finite lattice containing 5 elements)

See also

Stronger properties: is_join_semidistributive(), is_meet_semidistributive()
Weaker properties: is_sublattice_dismantlable()

is_isoform(certificate=False)[source]¶

Return True if the lattice is isoform and False otherwise.

A congruence is isoform (or isotype) if all blocks are isomorphic sublattices. A lattice is isoform if it has only isoform congruences.

INPUT:

certificate – boolean (default: False); whether to return a certificate if the lattice is not isoform

OUTPUT:

If certificate=True return either (True, None) or (False, C), where \(C\) is a non-isoform congruence as a sage.combinat.set_partition.SetPartition. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [5, 6], 3: [6, 7],
....:                   4: [7], 5: [8], 6: [8], 7: [8]})
sage: L.is_isoform()                                                        # needs sage.combinat
True

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5), Integer(6)], Integer(3): [Integer(6), Integer(7)],
...                   Integer(4): [Integer(7)], Integer(5): [Integer(8)], Integer(6): [Integer(8)], Integer(7): [Integer(8)]})
>>> L.is_isoform()                                                        # needs sage.combinat
True

Every isoform lattice is (trivially) uniform, but the converse is not true:

Sage

sage: L = LatticePoset({1: [2, 3, 6], 2: [4, 5], 3: [5], 4: [9, 8],
....:                   5: [7, 8], 6: [9], 7: [10], 8: [10], 9: [10]})
sage: L.is_isoform(), L.is_uniform()                                        # needs sage.combinat
(False, True)

sage: L.is_isoform(certificate=True)                                        # needs sage.combinat
(False, {{1, 2, 4, 6, 9}, {3, 5, 7, 8, 10}})

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(6)], Integer(2): [Integer(4), Integer(5)], Integer(3): [Integer(5)], Integer(4): [Integer(9), Integer(8)],
...                   Integer(5): [Integer(7), Integer(8)], Integer(6): [Integer(9)], Integer(7): [Integer(10)], Integer(8): [Integer(10)], Integer(9): [Integer(10)]})
>>> L.is_isoform(), L.is_uniform()                                        # needs sage.combinat
(False, True)

>>> L.is_isoform(certificate=True)                                        # needs sage.combinat
(False, {{1, 2, 4, 6, 9}, {3, 5, 7, 8, 10}})

See also

Weaker properties: is_uniform()
Stronger properties: is_simple(), is_relatively_complemented()
Other: congruence()

is_join_distributive(certificate=False)[source]¶

Return True if the lattice is join-distributive and False otherwise.

A lattice is join-distributive if every interval from an element to the join of the element’s upper covers is a distributive lattice. Actually this distributive sublattice is then a Boolean lattice.

They are also called as Dilworth’s lattices and upper locally distributive lattices. They can be characterized in many other ways, see [Dil1940].

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, e), where \(e\) is an element such that the interval from \(e\) to the meet of upper covers of \(e\) is not distributive. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [5, 6], 3: [5, 7],
....:                   4: [6, 7], 5: [8, 9], 6: [9], 7: [9, 10],
....:                   8: [11], 9: [11], 10: [11]})
sage: L.is_join_distributive()
True

sage: L = LatticePoset({1: [2], 2: [3, 4], 3: [5], 4: [6],
....:                   5: [7], 6: [7]})
sage: L.is_join_distributive()
False
sage: L.is_join_distributive(certificate=True)
(False, 2)

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5), Integer(6)], Integer(3): [Integer(5), Integer(7)],
...                   Integer(4): [Integer(6), Integer(7)], Integer(5): [Integer(8), Integer(9)], Integer(6): [Integer(9)], Integer(7): [Integer(9), Integer(10)],
...                   Integer(8): [Integer(11)], Integer(9): [Integer(11)], Integer(10): [Integer(11)]})
>>> L.is_join_distributive()
True

>>> L = LatticePoset({Integer(1): [Integer(2)], Integer(2): [Integer(3), Integer(4)], Integer(3): [Integer(5)], Integer(4): [Integer(6)],
...                   Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.is_join_distributive()
False
>>> L.is_join_distributive(certificate=True)
(False, 2)

See also

Dual property: is_meet_distributive()
Weaker properties: is_meet_semidistributive(), is_upper_semimodular()
Stronger properties: is_distributive()

is_join_pseudocomplemented(certificate=False)[source]¶

Return True if the lattice is join-pseudocomplemented, and False otherwise.

A lattice is join-pseudocomplemented if every element \(e\) has a join-pseudocomplement \(e'\), i.e. the least element such that the join of \(e\) and \(e'\) is the top element.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, e), where e is an element without a join-pseudocomplement. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 5], 2: [3, 6], 3: [4], 4: [7],
....:                   5: [6], 6: [7]})
sage: L.is_join_pseudocomplemented()
True

sage: L = LatticePoset({1: [2, 3], 2: [4, 5, 6], 3: [6], 4: [7],
....:                   5: [7], 6: [7]})
sage: L.is_join_pseudocomplemented()
False
sage: L.is_join_pseudocomplemented(certificate=True)
(False, 4)

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(5)], Integer(2): [Integer(3), Integer(6)], Integer(3): [Integer(4)], Integer(4): [Integer(7)],
...                   Integer(5): [Integer(6)], Integer(6): [Integer(7)]})
>>> L.is_join_pseudocomplemented()
True

>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5), Integer(6)], Integer(3): [Integer(6)], Integer(4): [Integer(7)],
...                   Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.is_join_pseudocomplemented()
False
>>> L.is_join_pseudocomplemented(certificate=True)
(False, 4)

See also

Dual property: is_pseudocomplemented()
Stronger properties: is_join_semidistributive()

is_join_semidistributive(certificate=False)[source]¶

Return True if the lattice is join-semidistributive, and False otherwise.

A lattice is join-semidistributive if for all elements \(e, x, y\) in the lattice we have

\[e \vee x = e \vee y \implies e \vee x = e \vee (x \wedge y)\]

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, (e, x, y)) such that \(e \vee x = e \vee y\) but \(e \vee x \neq e \vee (x \wedge y)\). If certificate=False return True or False.

EXAMPLES:

Sage

sage: T4 = posets.TamariLattice(4)
sage: T4.is_join_semidistributive()
True
sage: L = LatticePoset({1:[2, 3], 2:[4, 5], 3:[5, 6],
....:                   4:[7], 5:[7], 6:[7]})
sage: L.is_join_semidistributive()
False
sage: L.is_join_semidistributive(certificate=True)
(False, (5, 4, 6))

Python

>>> from sage.all import *
>>> T4 = posets.TamariLattice(Integer(4))
>>> T4.is_join_semidistributive()
True
>>> L = LatticePoset({Integer(1):[Integer(2), Integer(3)], Integer(2):[Integer(4), Integer(5)], Integer(3):[Integer(5), Integer(6)],
...                   Integer(4):[Integer(7)], Integer(5):[Integer(7)], Integer(6):[Integer(7)]})
>>> L.is_join_semidistributive()
False
>>> L.is_join_semidistributive(certificate=True)
(False, (5, 4, 6))

See also

Dual property: is_meet_semidistributive()
Weaker properties: is_join_pseudocomplemented(), is_interval_dismantlable()
Stronger properties: is_semidistributive(), is_meet_distributive(), is_constructible_by_doublings() (by lower pseudo-intervals)

is_left_modular_element(x)[source]¶

Return True if x is a left modular element and False otherwise.

INPUT:

x – an element of the lattice

An element \(x\) in a lattice \(L\) is left modular if

\[(y \vee x) \wedge z = y \vee (x \wedge z)\]

for every \(y \leq z \in L\).

It is enough to check this condition on all cover relations \(y < z\).

EXAMPLES:

Sage

sage: P = posets.PentagonPoset()
sage: [i for i in P if P.is_left_modular_element(i)]
[0, 2, 3, 4]

Python

>>> from sage.all import *
>>> P = posets.PentagonPoset()
>>> [i for i in P if P.is_left_modular_element(i)]
[0, 2, 3, 4]

See also

Stronger properties: is_modular_element()

is_lower_semimodular(certificate=False)[source]¶

Return True if the lattice is lower semimodular and False otherwise.

A lattice is lower semimodular if any pair of elements with a common upper cover have also a common lower cover.

INPUT:

certificate – boolean (default: False); whether to return a certificate if the lattice is not lower semimodular

OUTPUT:

If certificate=False return True or False. If certificate=True return either (True, None) or (False, (a, b)), where \(a\) and \(b\) are covered by their join but do no cover their meet.

See Wikipedia article Semimodular_lattice

EXAMPLES:

Sage

sage: L = posets.DiamondPoset(5)
sage: L.is_lower_semimodular()
True

sage: L = posets.PentagonPoset()
sage: L.is_lower_semimodular()
False

sage: L = posets.ChainPoset(6)
sage: L.is_lower_semimodular()
True

sage: L = LatticePoset(DiGraph('IS?`?AAOE_@?C?_@??'))
sage: L.is_lower_semimodular(certificate=True)
(False, (4, 2))

Python

>>> from sage.all import *
>>> L = posets.DiamondPoset(Integer(5))
>>> L.is_lower_semimodular()
True

>>> L = posets.PentagonPoset()
>>> L.is_lower_semimodular()
False

>>> L = posets.ChainPoset(Integer(6))
>>> L.is_lower_semimodular()
True

>>> L = LatticePoset(DiGraph('IS?`?AAOE_@?C?_@??'))
>>> L.is_lower_semimodular(certificate=True)
(False, (4, 2))

See also

Dual property: is_upper_semimodular()
Weaker properties: is_graded()
Stronger properties: is_modular(), is_meet_distributive()

is_meet_distributive(certificate=False)[source]¶

Return True if the lattice is meet-distributive and False otherwise.

A lattice is meet-distributive if every interval to an element from the meet of the element’s lower covers is a distributive lattice. Actually this distributive sublattice is then a Boolean lattice.

They are also called as lower locally distributive lattices. They can be characterized in many other ways, see [Dil1940].

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, e), where \(e\) is an element such that the interval to \(e\) from the meet of lower covers of \(e\) is not distributive. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [5], 3: [5, 6, 7],
....:                   4: [7], 5: [9, 8], 6: [10, 8], 7:
....:                   [9, 10], 8: [11], 9: [11], 10: [11]})
sage: L.is_meet_distributive()
True

sage: L = LatticePoset({1: [2, 3], 2: [4], 3: [5], 4: [6],
....:                   5: [6], 6: [7]})
sage: L.is_meet_distributive()
False
sage: L.is_meet_distributive(certificate=True)
(False, 6)

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5)], Integer(3): [Integer(5), Integer(6), Integer(7)],
...                   Integer(4): [Integer(7)], Integer(5): [Integer(9), Integer(8)], Integer(6): [Integer(10), Integer(8)], Integer(7):
...                   [Integer(9), Integer(10)], Integer(8): [Integer(11)], Integer(9): [Integer(11)], Integer(10): [Integer(11)]})
>>> L.is_meet_distributive()
True

>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4)], Integer(3): [Integer(5)], Integer(4): [Integer(6)],
...                   Integer(5): [Integer(6)], Integer(6): [Integer(7)]})
>>> L.is_meet_distributive()
False
>>> L.is_meet_distributive(certificate=True)
(False, 6)

See also

Dual property: is_join_distributive()
Weaker properties: is_join_semidistributive(), is_lower_semimodular()
Stronger properties: is_distributive()

is_meet_semidistributive(certificate=False)[source]¶

Return True if the lattice is meet-semidistributive, and False otherwise.

A lattice is meet-semidistributive if for all elements \(e, x, y\) in the lattice we have

\[e \wedge x = e \wedge y \implies e \wedge x = e \wedge (x \vee y)\]

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, (e, x, y)) such that \(e \wedge x = e \wedge y\) but \(e \wedge x \neq e \wedge (x \vee y)\). If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1:[2, 3, 4], 2:[4, 5], 3:[5, 6],
....:                   4:[7], 5:[7], 6:[7]})
sage: L.is_meet_semidistributive()
True
sage: L_ = L.dual()
sage: L_.is_meet_semidistributive()
False
sage: L_.is_meet_semidistributive(certificate=True)
(False, (5, 4, 6))

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1):[Integer(2), Integer(3), Integer(4)], Integer(2):[Integer(4), Integer(5)], Integer(3):[Integer(5), Integer(6)],
...                   Integer(4):[Integer(7)], Integer(5):[Integer(7)], Integer(6):[Integer(7)]})
>>> L.is_meet_semidistributive()
True
>>> L_ = L.dual()
>>> L_.is_meet_semidistributive()
False
>>> L_.is_meet_semidistributive(certificate=True)
(False, (5, 4, 6))

See also

Dual property: is_join_semidistributive()
Weaker properties: is_pseudocomplemented(), is_interval_dismantlable()
Stronger properties: is_semidistributive(), is_join_distributive(), is_constructible_by_doublings() (by upper pseudo-intervals)

is_modular(L=None, certificate=False)[source]¶

Return True if the lattice is modular and False otherwise.

An element \(b\) of a lattice is modular if

\[x \vee (a \wedge b) = (x \vee a) \wedge b\]

for every element \(x \leq b\) and \(a\). A lattice is modular if every element is modular. There are other equivalent definitions, see Wikipedia article Modular_lattice.

With the parameter L this can be used to check that some subset of elements are all modular.

INPUT:

L – (default: None) a list of elements to check being modular, if L is None, then this checks the entire lattice
certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, (x, a, b)), where \(a\), \(b\) and \(x\) are elements of the lattice such that \(x < b\) but \(x \vee (a \wedge b) \neq (x \vee a) \wedge b\). If also \(L\) is given then \(b\) in the certificate will be an element of \(L\). If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = posets.DiamondPoset(5)
sage: L.is_modular()
True

sage: L = posets.PentagonPoset()
sage: L.is_modular()
False

sage: L = LatticePoset({1:[2,3],2:[4,5],3:[5,6],4:[7],5:[7],6:[7]})
sage: L.is_modular(certificate=True)
(False, (2, 6, 4))
sage: [L.is_modular([x]) for x in L]
[True, True, False, True, True, False, True]

Python

>>> from sage.all import *
>>> L = posets.DiamondPoset(Integer(5))
>>> L.is_modular()
True

>>> L = posets.PentagonPoset()
>>> L.is_modular()
False

>>> L = LatticePoset({Integer(1):[Integer(2),Integer(3)],Integer(2):[Integer(4),Integer(5)],Integer(3):[Integer(5),Integer(6)],Integer(4):[Integer(7)],Integer(5):[Integer(7)],Integer(6):[Integer(7)]})
>>> L.is_modular(certificate=True)
(False, (2, 6, 4))
>>> [L.is_modular([x]) for x in L]
[True, True, False, True, True, False, True]

See also

Weaker properties: is_upper_semimodular(), is_lower_semimodular(), is_supersolvable()
Stronger properties: is_distributive()
Other: is_modular_element()

is_modular_element(x)[source]¶

Return True if x is a modular element and False otherwise.

INPUT:

x – an element of the lattice

An element \(x\) in a lattice \(L\) is modular if \(x \leq b\) implies

\[x \vee (a \wedge b) = (x \vee a) \wedge b\]

for every \(a, b \in L\).

EXAMPLES:

Sage

sage: L = LatticePoset({1:[2,3],2:[4,5],3:[5,6],4:[7],5:[7],6:[7]})
sage: L.is_modular()
False
sage: [L.is_modular_element(x) for x in L]
[True, True, False, True, True, False, True]

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1):[Integer(2),Integer(3)],Integer(2):[Integer(4),Integer(5)],Integer(3):[Integer(5),Integer(6)],Integer(4):[Integer(7)],Integer(5):[Integer(7)],Integer(6):[Integer(7)]})
>>> L.is_modular()
False
>>> [L.is_modular_element(x) for x in L]
[True, True, False, True, True, False, True]

See also

Weaker properties: is_left_modular_element()
Other: is_modular() to check modularity for the full lattice or some set of elements

is_orthocomplemented(unique=False)[source]¶

Return True if the lattice admits an orthocomplementation, and False otherwise.

An orthocomplementation of a lattice is a function defined for every element \(e\) and marked as \(e^{\bot}\) such that 1) they are complements, i.e. \(e \vee e^{\bot}\) is the top element and \(e \wedge e^{\bot}\) is the bottom element, 2) it is involution, i.e. \({(e^{\bot})}^{\bot} = e\), and 3) it is order-reversing, i.e. if \(a < b\) then \(b^{\bot} < a^{\bot}\).

INPUT:

unique – boolean; if True, return True only if the lattice has exactly one orthocomplementation. If False (the default), return True when the lattice has at least one orthocomplementation.

EXAMPLES:

Sage

sage: D5 = posets.DiamondPoset(5)
sage: D5.is_orthocomplemented()
False

sage: D6 = posets.DiamondPoset(6)
sage: D6.is_orthocomplemented()                                             # needs sage.groups
True
sage: D6.is_orthocomplemented(unique=True)                                  # needs sage.groups
False

sage: hexagon = LatticePoset({0: [1, 2], 1: [3], 2: [4], 3:[5], 4: [5]})
sage: hexagon.is_orthocomplemented(unique=True)                             # needs sage.groups
True

Python

>>> from sage.all import *
>>> D5 = posets.DiamondPoset(Integer(5))
>>> D5.is_orthocomplemented()
False

>>> D6 = posets.DiamondPoset(Integer(6))
>>> D6.is_orthocomplemented()                                             # needs sage.groups
True
>>> D6.is_orthocomplemented(unique=True)                                  # needs sage.groups
False

>>> hexagon = LatticePoset({Integer(0): [Integer(1), Integer(2)], Integer(1): [Integer(3)], Integer(2): [Integer(4)], Integer(3):[Integer(5)], Integer(4): [Integer(5)]})
>>> hexagon.is_orthocomplemented(unique=True)                             # needs sage.groups
True

See also

Weaker properties: is_complemented(), is_self_dual()

is_planar()[source]¶

Return True if the lattice is upward planar, and False otherwise.

A lattice is upward planar if its Hasse diagram has a planar drawing in the \(\mathbb{R}^2\) plane, in such a way that \(x\) is strictly below \(y\) (on the vertical axis) whenever \(x<y\) in the lattice.

Note that the scientific literature on posets often omits “upward” and shortens it to “planar lattice” (e.g. [GW2014]), which can cause confusion with the notion of graph planarity in graph theory.

Note

Not all lattices which are planar – in the sense of graph planarity – admit such a planar drawing (see example below).

ALGORITHM:

Using the result from [Platt1976], this method returns its result by testing that the Hasse diagram of the lattice is planar (in the sense of graph theory) when an edge is added between the top and bottom elements.

EXAMPLES:

The Boolean lattice of \(2^3\) elements is not upward planar, even if its covering relations graph is planar:

Sage

sage: B3 = posets.BooleanLattice(3)
sage: B3.is_planar()
False
sage: G = B3.cover_relations_graph()
sage: G.is_planar()
True

Python

>>> from sage.all import *
>>> B3 = posets.BooleanLattice(Integer(3))
>>> B3.is_planar()
False
>>> G = B3.cover_relations_graph()
>>> G.is_planar()
True

Ordinal product of planar lattices is obviously planar. Same does not apply to Cartesian products:

Sage

sage: P = posets.PentagonPoset()
sage: Pc = P.product(P)
sage: Po = P.ordinal_product(P)
sage: Pc.is_planar()
False
sage: Po.is_planar()
True

Python

>>> from sage.all import *
>>> P = posets.PentagonPoset()
>>> Pc = P.product(P)
>>> Po = P.ordinal_product(P)
>>> Pc.is_planar()
False
>>> Po.is_planar()
True

See also

Weaker properties: is_dismantlable()

is_pseudocomplemented(certificate=False)[source]¶

Return True if the lattice is pseudocomplemented, and False otherwise.

A lattice is (meet-)pseudocomplemented if every element \(e\) has a pseudocomplement \(e^\star\), i.e. the greatest element such that the meet of \(e\) and \(e^\star\) is the bottom element.

See Wikipedia article Pseudocomplement.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, e), where e is an element without a pseudocomplement. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 5], 2: [3, 6], 3: [4], 4: [7],
....:                   5: [6], 6: [7]})
sage: L.is_pseudocomplemented()
True

sage: L = LatticePoset({1: [2, 3], 2: [4, 5, 6], 3: [6], 4: [7],
....:                   5: [7], 6: [7]})
sage: L.is_pseudocomplemented()
False
sage: L.is_pseudocomplemented(certificate=True)
(False, 3)

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(5)], Integer(2): [Integer(3), Integer(6)], Integer(3): [Integer(4)], Integer(4): [Integer(7)],
...                   Integer(5): [Integer(6)], Integer(6): [Integer(7)]})
>>> L.is_pseudocomplemented()
True

>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5), Integer(6)], Integer(3): [Integer(6)], Integer(4): [Integer(7)],
...                   Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.is_pseudocomplemented()
False
>>> L.is_pseudocomplemented(certificate=True)
(False, 3)

See also

Dual property: is_join_pseudocomplemented()
Stronger properties: is_meet_semidistributive()
Other: pseudocomplement().

ALGORITHM:

According to [Cha92] a lattice is pseudocomplemented if and only if every atom has a pseudocomplement. So we only check those.

is_regular(certificate=False)[source]¶

Return True if the lattice is regular and False otherwise.

A congruence of a lattice is regular if it is generated by any of its parts. A lattice is regular if it has only regular congruences.

INPUT:

certificate – boolean (default: False); whether to return a certificate if the lattice is not regular

OUTPUT:

If certificate=True return either (True, None) or (False, (C, p)), where \(C\) is a non-regular congruence as a sage.combinat.set_partition.SetPartition and \(p\) is a congruence class of \(C\) such that the congruence generated by \(p\) is not \(C\). If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [5, 6], 3: [8, 7], 4: [6, 7],
....:                   5: [8], 6: [9], 7: [9], 8: [9]})
sage: L.is_regular()                                                        # needs sage.combinat
True

sage: N5 = posets.PentagonPoset()
sage: N5.is_regular()                                                       # needs sage.combinat
False
sage: N5.is_regular(certificate=True)                                       # needs sage.combinat
(False, ({{0}, {1}, {2, 3}, {4}}, [0]))

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5), Integer(6)], Integer(3): [Integer(8), Integer(7)], Integer(4): [Integer(6), Integer(7)],
...                   Integer(5): [Integer(8)], Integer(6): [Integer(9)], Integer(7): [Integer(9)], Integer(8): [Integer(9)]})
>>> L.is_regular()                                                        # needs sage.combinat
True

>>> N5 = posets.PentagonPoset()
>>> N5.is_regular()                                                       # needs sage.combinat
False
>>> N5.is_regular(certificate=True)                                       # needs sage.combinat
(False, ({{0}, {1}, {2, 3}, {4}}, [0]))

See also

Stronger properties: is_uniform(), is_sectionally_complemented(), is_cosectionally_complemented()
Mutually exclusive properties: is_vertically_decomposable()
Other: congruence()

is_relatively_complemented(certificate=False)[source]¶

Return True if the lattice is relatively complemented, and False otherwise.

A lattice is relatively complemented if every interval of it is a complemented lattice.

INPUT:

certificate – boolean (default: False); whether to return a certificate if the lattice is not relatively complemented

OUTPUT:

If certificate=True return either (True, None) or (False, (a, b, c)), where \(b\) is the only element that covers \(a\) and is covered by \(c\). If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4, 8], 2: [5, 6], 3: [5, 7],
....:                   4: [6, 7], 5: [9], 6: [9], 7: [9], 8: [9]})
sage: L.is_relatively_complemented()
True

sage: L = posets.PentagonPoset()
sage: L.is_relatively_complemented()
False

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4), Integer(8)], Integer(2): [Integer(5), Integer(6)], Integer(3): [Integer(5), Integer(7)],
...                   Integer(4): [Integer(6), Integer(7)], Integer(5): [Integer(9)], Integer(6): [Integer(9)], Integer(7): [Integer(9)], Integer(8): [Integer(9)]})
>>> L.is_relatively_complemented()
True

>>> L = posets.PentagonPoset()
>>> L.is_relatively_complemented()
False

Relatively complemented lattice must be both atomic and coatomic. Implication to other direction does not hold:

Sage

sage: L = LatticePoset({0: [1, 2, 3, 4, 5], 1: [6, 7], 2: [6, 8],
....:                   3: [7, 8, 9], 4: [9, 11], 5: [9, 10],
....:                   6: [10, 11], 7: [12], 8: [12], 9: [12],
....:                   10: [12], 11: [12]})
sage: L.is_atomic() and L.is_coatomic()
True
sage: L.is_relatively_complemented()
False

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(0): [Integer(1), Integer(2), Integer(3), Integer(4), Integer(5)], Integer(1): [Integer(6), Integer(7)], Integer(2): [Integer(6), Integer(8)],
...                   Integer(3): [Integer(7), Integer(8), Integer(9)], Integer(4): [Integer(9), Integer(11)], Integer(5): [Integer(9), Integer(10)],
...                   Integer(6): [Integer(10), Integer(11)], Integer(7): [Integer(12)], Integer(8): [Integer(12)], Integer(9): [Integer(12)],
...                   Integer(10): [Integer(12)], Integer(11): [Integer(12)]})
>>> L.is_atomic() and L.is_coatomic()
True
>>> L.is_relatively_complemented()
False

We can also get a non-complemented 3-element interval:

Sage

sage: L.is_relatively_complemented(certificate=True)
(False, (1, 6, 11))

Python

>>> from sage.all import *
>>> L.is_relatively_complemented(certificate=True)
(False, (1, 6, 11))

See also

Weaker properties: is_sectionally_complemented(), is_cosectionally_complemented(), is_isoform()
Stronger properties: is_geometric()

is_sectionally_complemented(certificate=False)[source]¶

Return True if the lattice is sectionally complemented, and False otherwise.

A lattice is sectionally complemented if all intervals from the bottom element interpreted as sublattices are complemented lattices.

INPUT:

certificate – boolean (default: False); whether to return a certificate if the lattice is not sectionally complemented

OUTPUT:

If certificate=False return True or False. If certificate=True return either (True, None) or (False, (t, e)), where \(t\) is an element so that in the sublattice from the bottom element to \(t\) has no complement for element \(e\).

EXAMPLES:

Smallest examples of a complemented but not sectionally complemented lattice and a sectionally complemented but not relatively complemented lattice:

Sage

sage: L = posets.PentagonPoset()
sage: L.is_complemented()
True
sage: L.is_sectionally_complemented()
False

sage: L = LatticePoset({0: [1, 2, 3], 1: [4], 2: [4], 3: [5], 4: [5]})
sage: L.is_sectionally_complemented()
True
sage: L.is_relatively_complemented()
False

Python

>>> from sage.all import *
>>> L = posets.PentagonPoset()
>>> L.is_complemented()
True
>>> L.is_sectionally_complemented()
False

>>> L = LatticePoset({Integer(0): [Integer(1), Integer(2), Integer(3)], Integer(1): [Integer(4)], Integer(2): [Integer(4)], Integer(3): [Integer(5)], Integer(4): [Integer(5)]})
>>> L.is_sectionally_complemented()
True
>>> L.is_relatively_complemented()
False

Getting a certificate:

Sage

sage: L = LatticePoset(DiGraph('HYOgC?C@?C?G@??'))
sage: L.is_sectionally_complemented(certificate=True)
(False, (6, 1))

Python

>>> from sage.all import *
>>> L = LatticePoset(DiGraph('HYOgC?C@?C?G@??'))
>>> L.is_sectionally_complemented(certificate=True)
(False, (6, 1))

See also

Dual property: is_cosectionally_complemented()
Weaker properties: is_complemented(), is_atomic(), is_regular()
Stronger properties: is_relatively_complemented()

is_semidistributive()[source]¶

Return True if the lattice is both join- and meet-semidistributive, and False otherwise.

EXAMPLES:

Tamari lattices are typical examples of semidistributive but not distributive (and hence not modular) lattices:

Sage

sage: T4 = posets.TamariLattice(4)
sage: T4.is_semidistributive(), T4.is_distributive()
(True, False)

Python

>>> from sage.all import *
>>> T4 = posets.TamariLattice(Integer(4))
>>> T4.is_semidistributive(), T4.is_distributive()
(True, False)

Smallest non-selfdual example:

Sage

sage: L = LatticePoset({1: [2, 3], 2: [4, 5], 3: [5], 4: [6], 5: [7], 6: [7]})
sage: L.is_semidistributive()
True

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5)], Integer(3): [Integer(5)], Integer(4): [Integer(6)], Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.is_semidistributive()
True

The diamond is not semidistributive:

Sage

sage: L = posets.DiamondPoset(5)
sage: L.is_semidistributive()
False

Python

>>> from sage.all import *
>>> L = posets.DiamondPoset(Integer(5))
>>> L.is_semidistributive()
False

See also

Weaker properties: is_join_semidistributive(), is_meet_semidistributive()
Stronger properties: is_distributive()

is_simple(certificate=False)[source]¶

Return True if the lattice is simple and False otherwise.

A lattice is simple if it has no nontrivial congruences; in other words, for every two distinct elements \(a\) and \(b\) the principal congruence generated by \((a, b)\) has only one component, i.e. the whole lattice.

INPUT:

certificate – boolean (default: False); whether to return a certificate if the lattice is not simple

OUTPUT:

If certificate=True return either (True, None) or (False, c), where \(c\) is a nontrivial congruence as a sage.combinat.set_partition.SetPartition. If certificate=False return True or False.

EXAMPLES:

Sage

sage: # needs sage.combinat
sage: posets.DiamondPoset(5).is_simple()  # Smallest nontrivial example
True
sage: L = LatticePoset({1: [2, 3], 2: [4, 5], 3: [6], 4: [6], 5: [6]})
sage: L.is_simple()
False
sage: L.is_simple(certificate=True)
(False, {{1, 3}, {2, 4, 5, 6}})

Python

>>> from sage.all import *
>>> # needs sage.combinat
>>> posets.DiamondPoset(Integer(5)).is_simple()  # Smallest nontrivial example
True
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5)], Integer(3): [Integer(6)], Integer(4): [Integer(6)], Integer(5): [Integer(6)]})
>>> L.is_simple()
False
>>> L.is_simple(certificate=True)
(False, {{1, 3}, {2, 4, 5, 6}})

Two more examples. First is a non-simple lattice without any 2-element congruences:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [5], 3: [5], 4: [6, 7],
....:                   5: [8], 6: [8], 7: [8]})
sage: L.is_simple()                                                         # needs sage.combinat
False
sage: L = LatticePoset({1: [2, 3], 2: [4, 5], 3: [6, 7], 4: [8],
....:                   5: [8], 6: [8], 7: [8]})
sage: L.is_simple()                                                         # needs sage.combinat
True

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5)], Integer(3): [Integer(5)], Integer(4): [Integer(6), Integer(7)],
...                   Integer(5): [Integer(8)], Integer(6): [Integer(8)], Integer(7): [Integer(8)]})
>>> L.is_simple()                                                         # needs sage.combinat
False
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5)], Integer(3): [Integer(6), Integer(7)], Integer(4): [Integer(8)],
...                   Integer(5): [Integer(8)], Integer(6): [Integer(8)], Integer(7): [Integer(8)]})
>>> L.is_simple()                                                         # needs sage.combinat
True

See also

Weaker properties: is_isoform()
Mutually exclusive properties: is_constructible_by_doublings() (by any set)
Other: congruence()

is_stone(certificate=False)[source]¶

Return True if the lattice is a Stone lattice, and False otherwise.

The lattice is expected to be distributive (and hence pseudocomplemented).

A pseudocomplemented lattice is a Stone lattice if

\[e^* \vee e^{**} = \top\]

for every element \(e\) of the lattice, where \(^*\) is the pseudocomplement and \(\top\) is the top element of the lattice.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (True, None) or (False, e) such that \(e^* \vee e^{**} \neq \top\). If certificate=False return True or False.

EXAMPLES:

Divisor lattices are canonical example:

Sage

sage: D72 = posets.DivisorLattice(72)
sage: D72.is_stone()
True

Python

>>> from sage.all import *
>>> D72 = posets.DivisorLattice(Integer(72))
>>> D72.is_stone()
True

A non-example:

Sage

sage: L = LatticePoset({1: [2, 3], 2: [4], 3: [4], 4: [5]})
sage: L.is_stone()
False

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4)], Integer(3): [Integer(4)], Integer(4): [Integer(5)]})
>>> L.is_stone()
False

See also

Weaker properties: is_distributive()

is_subdirectly_reducible(certificate=False)[source]¶

Return True if the lattice is subdirectly reducible.

A lattice \(M\) is a subdirect product of \(K\) and \(L\) if it is a sublattice of \(K \times L\). Lattice \(M\) is subdirectly reducible if there exists such lattices \(K\) and \(L\) so that \(M\) is not a sublattice of either.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

if certificate=False, return only True or False
if certificate=True, return either
- (True, (K, L)) such that the lattice is isomorphic to a sublattice of \(K \times L\).
- (False, (a, b)), where \(a\) and \(b\) are elements that are in the same congruence class for every nontrivial congruence of the lattice. Special case: If the lattice has zero or one element, return (False, None).

EXAMPLES:

Sage

sage: N5 = posets.PentagonPoset()
sage: N5.is_subdirectly_reducible()                                         # needs sage.combinat
False

sage: hex = LatticePoset({1: [2, 3], 2: [4], 3: [5], 4: [6], 5: [6]})
sage: hex.is_subdirectly_reducible()                                        # needs sage.combinat
True

sage: hex.is_subdirectly_reducible(certificate=True)                        # needs sage.combinat
(True,
 (Finite lattice containing 5 elements, Finite lattice containing 5 elements))

sage: N5.is_subdirectly_reducible(certificate=True)                         # needs sage.combinat
(False, (2, 3))
sage: res, cert = hex.is_subdirectly_reducible(certificate=True)            # needs sage.combinat
sage: cert[0].is_isomorphic(N5)                                             # needs sage.combinat
True

Python

>>> from sage.all import *
>>> N5 = posets.PentagonPoset()
>>> N5.is_subdirectly_reducible()                                         # needs sage.combinat
False

>>> hex = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4)], Integer(3): [Integer(5)], Integer(4): [Integer(6)], Integer(5): [Integer(6)]})
>>> hex.is_subdirectly_reducible()                                        # needs sage.combinat
True

>>> hex.is_subdirectly_reducible(certificate=True)                        # needs sage.combinat
(True,
 (Finite lattice containing 5 elements, Finite lattice containing 5 elements))

>>> N5.is_subdirectly_reducible(certificate=True)                         # needs sage.combinat
(False, (2, 3))
>>> res, cert = hex.is_subdirectly_reducible(certificate=True)            # needs sage.combinat
>>> cert[Integer(0)].is_isomorphic(N5)                                             # needs sage.combinat
True

See also

Stronger properties: is_distributive(), is_vertically_decomposable()
Other: subdirect_decomposition()

is_sublattice(other)[source]¶

Return True if the lattice is a sublattice of other, and False otherwise.

Lattice \(K\) is a sublattice of \(L\) if \(K\) is an (induced) subposet of \(L\) and closed under meet and join of \(L\).

Note

This method does not check whether the lattice is a isomorphic (i.e., up to relabeling) sublattice of other, but only if other directly contains the lattice as an sublattice.

EXAMPLES:

A pentagon sublattice in a non-modular lattice:

Sage

sage: L = LatticePoset({1: [2, 3], 2: [4, 5], 3: [5, 6], 4: [7], 5: [7], 6: [7]})
sage: N5 = LatticePoset({1: [2, 6], 2: [4], 4: [7], 6: [7]})
sage: N5.is_sublattice(L)
True

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5)], Integer(3): [Integer(5), Integer(6)], Integer(4): [Integer(7)], Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> N5 = LatticePoset({Integer(1): [Integer(2), Integer(6)], Integer(2): [Integer(4)], Integer(4): [Integer(7)], Integer(6): [Integer(7)]})
>>> N5.is_sublattice(L)
True

This pentagon is a subposet but not closed under join, hence not a sublattice:

Sage

sage: N5_ = LatticePoset({1: [2, 3], 2: [4], 3: [7], 4: [7]})
sage: N5_.is_induced_subposet(L)
True
sage: N5_.is_sublattice(L)
False

Python

>>> from sage.all import *
>>> N5_ = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4)], Integer(3): [Integer(7)], Integer(4): [Integer(7)]})
>>> N5_.is_induced_subposet(L)
True
>>> N5_.is_sublattice(L)
False

See also

isomorphic_sublattices_iterator()

is_sublattice_dismantlable()[source]¶

Return True if the lattice is sublattice dismantlable, and False otherwise.

A sublattice dismantling is a subdivision of a lattice into two non-empty sublattices. A lattice is sublattice dismantlable if it can be decomposed into 1-element lattices by consecutive sublattice dismantlings.

EXAMPLES:

The smallest non-example is this (and the dual):

Sage

sage: P = Poset({1: [11, 12, 13], 2: [11, 14, 15],
....:            3: [12, 14, 16], 4: [13, 15, 16]})
sage: L = LatticePoset(P.with_bounds())
sage: L.is_sublattice_dismantlable()
False

Python

>>> from sage.all import *
>>> P = Poset({Integer(1): [Integer(11), Integer(12), Integer(13)], Integer(2): [Integer(11), Integer(14), Integer(15)],
...            Integer(3): [Integer(12), Integer(14), Integer(16)], Integer(4): [Integer(13), Integer(15), Integer(16)]})
>>> L = LatticePoset(P.with_bounds())
>>> L.is_sublattice_dismantlable()
False

Here we adjoin a (double-irreducible-)dismantlable lattice as a part to an interval-dismantlable lattice:

Sage

sage: B3 = posets.BooleanLattice(3)
sage: N5 = posets.PentagonPoset()
sage: L = B3.adjunct(N5, 1, 7)
sage: L.is_dismantlable(), L.is_interval_dismantlable()
(False, False)
sage: L.is_sublattice_dismantlable()
True

Python

>>> from sage.all import *
>>> B3 = posets.BooleanLattice(Integer(3))
>>> N5 = posets.PentagonPoset()
>>> L = B3.adjunct(N5, Integer(1), Integer(7))
>>> L.is_dismantlable(), L.is_interval_dismantlable()
(False, False)
>>> L.is_sublattice_dismantlable()
True

See also

Stronger properties: is_dismantlable(), is_interval_dismantlable()

Todo

Add a certificate-option.

is_supersolvable(certificate=False)[source]¶

Return True if the lattice is supersolvable, and False otherwise.

A lattice \(L\) is supersolvable if there exists a maximal chain \(C\) such that every \(x \in C\) is a modular element in \(L\). Equivalent definition is that the sublattice generated by \(C\) and any other chain is distributive.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (False, None) or (True, C), where C is a maximal chain of modular elements. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = posets.DiamondPoset(5)
sage: L.is_supersolvable()
True

sage: L = posets.PentagonPoset()
sage: L.is_supersolvable()
False

sage: L = LatticePoset({1:[2,3],2:[4,5],3:[5,6],4:[7],5:[7],6:[7]})
sage: L.is_supersolvable()
True
sage: L.is_supersolvable(certificate=True)
(True, [1, 2, 5, 7])
sage: L.is_modular()
False

sage: L = LatticePoset({0: [1, 2, 3, 4], 1: [5, 6, 7],
....:                   2: [5, 8, 9], 3: [6, 8, 10], 4: [7, 9, 10],
....:                   5: [11], 6: [11], 7: [11], 8: [11],
....:                   9: [11], 10: [11]})
sage: L.is_supersolvable()
False

Python

>>> from sage.all import *
>>> L = posets.DiamondPoset(Integer(5))
>>> L.is_supersolvable()
True

>>> L = posets.PentagonPoset()
>>> L.is_supersolvable()
False

>>> L = LatticePoset({Integer(1):[Integer(2),Integer(3)],Integer(2):[Integer(4),Integer(5)],Integer(3):[Integer(5),Integer(6)],Integer(4):[Integer(7)],Integer(5):[Integer(7)],Integer(6):[Integer(7)]})
>>> L.is_supersolvable()
True
>>> L.is_supersolvable(certificate=True)
(True, [1, 2, 5, 7])
>>> L.is_modular()
False

>>> L = LatticePoset({Integer(0): [Integer(1), Integer(2), Integer(3), Integer(4)], Integer(1): [Integer(5), Integer(6), Integer(7)],
...                   Integer(2): [Integer(5), Integer(8), Integer(9)], Integer(3): [Integer(6), Integer(8), Integer(10)], Integer(4): [Integer(7), Integer(9), Integer(10)],
...                   Integer(5): [Integer(11)], Integer(6): [Integer(11)], Integer(7): [Integer(11)], Integer(8): [Integer(11)],
...                   Integer(9): [Integer(11)], Integer(10): [Integer(11)]})
>>> L.is_supersolvable()
False

See also

Weaker properties: is_graded()
Stronger properties: is_modular()

is_trim(certificate=False)[source]¶

Return whether a lattice is trim.

A lattice is trim if it is extremal and left modular.

This notion is defined in [Thom2006].

INPUT:

certificate – boolean (default: False); whether to return instead a maximum chain of left modular elements

EXAMPLES:

Sage

sage: P = posets.PentagonPoset()
sage: P.is_trim()
True

sage: Q = LatticePoset(posets.SymmetricGroupWeakOrderPoset(3))
sage: Q.is_trim()
False

Python

>>> from sage.all import *
>>> P = posets.PentagonPoset()
>>> P.is_trim()
True

>>> Q = LatticePoset(posets.SymmetricGroupWeakOrderPoset(Integer(3)))
>>> Q.is_trim()
False

See also

Weaker properties: is_extremal()
Stronger properties: is_distributive()

REFERENCES:

[Thom2006]

Hugh Thomas, An analogue of distributivity for ungraded lattices. Order 23 (2006), no. 2-3, 249-269.

is_uniform(certificate=False)[source]¶

Return True if the lattice is uniform and False otherwise.

A congruence is uniform if all blocks have equal number of elements. A lattice is uniform if it has only uniform congruences.

INPUT:

certificate – boolean (default: False); whether to return a certificate if the lattice is not uniform

OUTPUT:

If certificate=True return either (True, None) or (False, C), where \(C\) is a non-uniform congruence as a sage.combinat.set_partition.SetPartition. If certificate=False return True or False.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [6, 7], 3: [5], 4: [5],
....:                   5: [9, 8], 6: [9], 7: [10], 8: [10], 9: [10]})
sage: L.is_uniform()                                                        # needs sage.combinat
True

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(6), Integer(7)], Integer(3): [Integer(5)], Integer(4): [Integer(5)],
...                   Integer(5): [Integer(9), Integer(8)], Integer(6): [Integer(9)], Integer(7): [Integer(10)], Integer(8): [Integer(10)], Integer(9): [Integer(10)]})
>>> L.is_uniform()                                                        # needs sage.combinat
True

Every uniform lattice is regular, but the converse is not true:

Sage

sage: N6 = LatticePoset({1: [2, 3, 5], 2: [4], 3: [4], 5: [6], 4: [6]})
sage: N6.is_uniform(), N6.is_regular()
(False, True)

sage: N6.is_uniform(certificate=True)                                       # needs sage.combinat
(False, {{1, 2, 3, 4}, {5, 6}})

Python

>>> from sage.all import *
>>> N6 = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(5)], Integer(2): [Integer(4)], Integer(3): [Integer(4)], Integer(5): [Integer(6)], Integer(4): [Integer(6)]})
>>> N6.is_uniform(), N6.is_regular()
(False, True)

>>> N6.is_uniform(certificate=True)                                       # needs sage.combinat
(False, {{1, 2, 3, 4}, {5, 6}})

See also

Weaker properties: is_regular()
Stronger properties: is_isoform()
Other: congruence()

is_upper_semimodular(certificate=False)[source]¶

Return True if the lattice is upper semimodular and False otherwise.

A lattice is upper semimodular if any pair of elements with a common lower cover have also a common upper cover.

INPUT:

certificate – boolean (default: False); whether to return a certificate if the lattice is not upper semimodular

OUTPUT:

If certificate=False return True or False. If certificate=True return either (True, None) or (False, (a, b)), where \(a\) and \(b\) covers their meet but are not covered by their join.

See Wikipedia article Semimodular_lattice

EXAMPLES:

Sage

sage: L = posets.DiamondPoset(5)
sage: L.is_upper_semimodular()
True

sage: L = posets.PentagonPoset()
sage: L.is_upper_semimodular()
False

sage: L = LatticePoset(posets.IntegerPartitions(4))                         # needs sage.combinat
sage: L.is_upper_semimodular()                                              # needs sage.combinat
True

sage: L = LatticePoset({1:[2, 3, 4], 2: [5], 3:[5, 6], 4:[6], 5:[7], 6:[7]})
sage: L.is_upper_semimodular(certificate=True)
(False, (4, 2))

Python

>>> from sage.all import *
>>> L = posets.DiamondPoset(Integer(5))
>>> L.is_upper_semimodular()
True

>>> L = posets.PentagonPoset()
>>> L.is_upper_semimodular()
False

>>> L = LatticePoset(posets.IntegerPartitions(Integer(4)))                         # needs sage.combinat
>>> L.is_upper_semimodular()                                              # needs sage.combinat
True

>>> L = LatticePoset({Integer(1):[Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5)], Integer(3):[Integer(5), Integer(6)], Integer(4):[Integer(6)], Integer(5):[Integer(7)], Integer(6):[Integer(7)]})
>>> L.is_upper_semimodular(certificate=True)
(False, (4, 2))

See also

Dual property: is_lower_semimodular()
Weaker properties: is_graded()
Stronger properties: is_modular(), is_join_distributive(), is_geometric()

is_vertically_decomposable(certificate=False)[source]¶

Return True if the lattice is vertically decomposable, and False otherwise.

A lattice is vertically decomposable if it has an element that is comparable to all elements and is neither the bottom nor the top element.

Informally said, a lattice is vertically decomposable if it can be seen as two lattices “glued” by unifying the top element of first lattice to the bottom element of second one.

INPUT:

certificate – boolean (default: False); whether to return a certificate

OUTPUT:

If certificate=True return either (False, None) or (True, e), where \(e\) is an element that is comparable to all other elements and is neither the bottom nor the top element. If certificate=False return True or False.

EXAMPLES:

Sage

sage: posets.TamariLattice(4).is_vertically_decomposable()
False
sage: L = LatticePoset( ([1, 2, 3, 6, 12, 18, 36],
....:     attrcall("divides")) )
sage: L.is_vertically_decomposable()
True
sage: L.is_vertically_decomposable(certificate=True)
(True, 6)

Python

>>> from sage.all import *
>>> posets.TamariLattice(Integer(4)).is_vertically_decomposable()
False
>>> L = LatticePoset( ([Integer(1), Integer(2), Integer(3), Integer(6), Integer(12), Integer(18), Integer(36)],
...     attrcall("divides")) )
>>> L.is_vertically_decomposable()
True
>>> L.is_vertically_decomposable(certificate=True)
(True, 6)

See also

Weaker properties: is_subdirectly_reducible()
Mutually exclusive properties: is_atomic(), is_coatomic(), is_regular()
Other: vertical_decomposition()

isomorphic_sublattices_iterator(other)[source]¶

Return an iterator over the sublattices of the lattice isomorphic to other.

INPUT:

other – a finite lattice

EXAMPLES:

A non-modular lattice contains a pentagon sublattice:

Sage

sage: L = LatticePoset({1: [2, 3], 2: [4, 5], 3: [5, 6], 4: [7], 5: [7], 6: [7]})
sage: L.is_modular()
False
sage: N5 = posets.PentagonPoset()
sage: N5_in_L = next(L.isomorphic_sublattices_iterator(N5)); N5_in_L
Finite lattice containing 5 elements
sage: N5_in_L.list()
[1, 3, 6, 4, 7]

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4), Integer(5)], Integer(3): [Integer(5), Integer(6)], Integer(4): [Integer(7)], Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.is_modular()
False
>>> N5 = posets.PentagonPoset()
>>> N5_in_L = next(L.isomorphic_sublattices_iterator(N5)); N5_in_L
Finite lattice containing 5 elements
>>> N5_in_L.list()
[1, 3, 6, 4, 7]

A divisor lattice is modular, hence does not contain the pentagon as sublattice, even if it has the pentagon subposet:

Sage

sage: D12 = posets.DivisorLattice(12)
sage: D12.has_isomorphic_subposet(N5)
True
sage: list(D12.isomorphic_sublattices_iterator(N5))
[]

Python

>>> from sage.all import *
>>> D12 = posets.DivisorLattice(Integer(12))
>>> D12.has_isomorphic_subposet(N5)
True
>>> list(D12.isomorphic_sublattices_iterator(N5))
[]

Warning

This function will return same sublattice as many times as there are automorphism on it. This is due to subgraph_search_iterator() returning labelled subgraphs.

join_primes()[source]¶

Return the join-prime elements of the lattice.

An element \(x\) of a lattice \(L\) is join-prime if \(x \le a \vee b\) implies \(x \le a\) or \(x \le b\) for every \(a, b \in L\).

These are also called coprime in some books. Every join-prime is join-irreducible; converse holds if and only if the lattice is distributive.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [5, 6], 3: [5],
....:                   4: [6], 5: [7], 6: [7]})
sage: L.join_primes()
[3, 4]

sage: D12 = posets.DivisorLattice(12)  # Distributive lattice
sage: D12.join_irreducibles() == D12.join_primes()
True

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5), Integer(6)], Integer(3): [Integer(5)],
...                   Integer(4): [Integer(6)], Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.join_primes()
[3, 4]

>>> D12 = posets.DivisorLattice(Integer(12))  # Distributive lattice
>>> D12.join_irreducibles() == D12.join_primes()
True

See also

Dual function: meet_primes()
Other: join_irreducibles()

maximal_sublattices()[source]¶

Return maximal (proper) sublattices of the lattice.

EXAMPLES:

Sage

sage: L = LatticePoset(( [], [[1,2],[1,17],[1,8],[2,3],[2,22],
....:                         [2,5],[2,7],[17,22],[17,13],[8,7],
....:                         [8,13],[3,16],[3,9],[22,16],[22,18],
....:                         [22,10],[5,18],[5,14],[7,9],[7,14],
....:                         [7,10],[13,10],[16,6],[16,19],[9,19],
....:                         [18,6],[18,33],[14,33],[10,19],
....:                         [10,33],[6,4],[19,4],[33,4]] ))
sage: maxs = L.maximal_sublattices()
sage: len(maxs)
7
sage: sorted(maxs[0].list())
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 14, 16, 18, 19, 22, 33]

Python

>>> from sage.all import *
>>> L = LatticePoset(( [], [[Integer(1),Integer(2)],[Integer(1),Integer(17)],[Integer(1),Integer(8)],[Integer(2),Integer(3)],[Integer(2),Integer(22)],
...                         [Integer(2),Integer(5)],[Integer(2),Integer(7)],[Integer(17),Integer(22)],[Integer(17),Integer(13)],[Integer(8),Integer(7)],
...                         [Integer(8),Integer(13)],[Integer(3),Integer(16)],[Integer(3),Integer(9)],[Integer(22),Integer(16)],[Integer(22),Integer(18)],
...                         [Integer(22),Integer(10)],[Integer(5),Integer(18)],[Integer(5),Integer(14)],[Integer(7),Integer(9)],[Integer(7),Integer(14)],
...                         [Integer(7),Integer(10)],[Integer(13),Integer(10)],[Integer(16),Integer(6)],[Integer(16),Integer(19)],[Integer(9),Integer(19)],
...                         [Integer(18),Integer(6)],[Integer(18),Integer(33)],[Integer(14),Integer(33)],[Integer(10),Integer(19)],
...                         [Integer(10),Integer(33)],[Integer(6),Integer(4)],[Integer(19),Integer(4)],[Integer(33),Integer(4)]] ))
>>> maxs = L.maximal_sublattices()
>>> len(maxs)
7
>>> sorted(maxs[Integer(0)].list())
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 14, 16, 18, 19, 22, 33]

meet_primes()[source]¶

Return the meet-prime elements of the lattice.

An element \(x\) of a lattice \(L\) is meet-prime if \(x \ge a \wedge b\) implies \(x \ge a\) or \(x \ge b\) for every \(a, b \in L\).

These are also called just prime in some books. Every meet-prime is meet-irreducible; converse holds if and only if the lattice is distributive.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2: [5, 6], 3: [5],
....:                   4: [6], 5: [7], 6: [7]})
sage: L.meet_primes()
[6, 5]

sage: D12 = posets.DivisorLattice(12)
sage: sorted(D12.meet_primes())
[3, 4, 6]

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2): [Integer(5), Integer(6)], Integer(3): [Integer(5)],
...                   Integer(4): [Integer(6)], Integer(5): [Integer(7)], Integer(6): [Integer(7)]})
>>> L.meet_primes()
[6, 5]

>>> D12 = posets.DivisorLattice(Integer(12))
>>> sorted(D12.meet_primes())
[3, 4, 6]

See also

Dual function: join_primes()
Other: meet_irreducibles()

moebius_algebra(R)[source]¶

Return the Möbius algebra of self over R.

OUTPUT: an instance of sage.combinat.posets.moebius_algebra.MoebiusAlgebra

EXAMPLES:

Sage

sage: L = posets.BooleanLattice(4)
sage: L.moebius_algebra(QQ)
Moebius algebra of Finite lattice containing 16 elements over Rational Field

Python

>>> from sage.all import *
>>> L = posets.BooleanLattice(Integer(4))
>>> L.moebius_algebra(QQ)
Moebius algebra of Finite lattice containing 16 elements over Rational Field

neutral_elements()[source]¶

Return the list of neutral elements of the lattice.

An element \(e\) of the lattice \(L\) is neutral if the sublattice generated by \(e\), \(x\) and \(y\) is distributive for all \(x, y \in L\). It can also be characterized as an element of intersection of maximal distributive sublattices.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3], 2: [6], 3: [4, 5, 6], 4: [8],
....:                   5: [7], 6: [7], 7: [8, 9], 8: [10], 9: [10]})
sage: L.neutral_elements()
[1, 3, 8, 10]

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(6)], Integer(3): [Integer(4), Integer(5), Integer(6)], Integer(4): [Integer(8)],
...                   Integer(5): [Integer(7)], Integer(6): [Integer(7)], Integer(7): [Integer(8), Integer(9)], Integer(8): [Integer(10)], Integer(9): [Integer(10)]})
>>> L.neutral_elements()
[1, 3, 8, 10]

quantum_moebius_algebra(q=None)[source]¶

Return the quantum Möbius algebra of self with parameter q.

INPUT:

q – (optional) the deformation parameter \(q\)

OUTPUT: an instance of sage.combinat.posets.moebius_algebra.QuantumMoebiusAlgebra

EXAMPLES:

Sage

sage: L = posets.BooleanLattice(4)
sage: L.quantum_moebius_algebra()
Quantum Moebius algebra of Finite lattice containing 16 elements
 with q=q over Univariate Laurent Polynomial Ring in q over Integer Ring

Python

>>> from sage.all import *
>>> L = posets.BooleanLattice(Integer(4))
>>> L.quantum_moebius_algebra()
Quantum Moebius algebra of Finite lattice containing 16 elements
 with q=q over Univariate Laurent Polynomial Ring in q over Integer Ring

quotient(congruence, labels='tuple')[source]¶

Return the quotient lattice by congruence.

Let \(L\) be a lattice and \(\Theta\) be a congruence of \(L\) with congruence classes \(\Theta_1, \Theta_2, \ldots\). The quotient lattice \(L/\Theta\) is the lattice with elements \(\{\Theta_1, \Theta_2, \ldots\}\) and meet and join given by the original lattice. Explicitly, if \(e_1 \in \Theta_1\) and \(e_2 \in \Theta_2\), such that \(e_1 \vee e_2 \in \Theta_3\) then \(\Theta_1 \vee \Theta_2 = \Theta_3\) in \(L/\Theta\) and similarly for meets.

INPUT:

congruence – list of lists; a congruence
labels – string; the elements of the resulting lattice and can be one of the following:
- 'tuple' – elements are tuples of elements of the original lattice
- 'lattice' – elements are sublattices of the original lattice
- 'integer' – elements are labeled by integers

Warning

congruence is expected to be a valid congruence of the lattice. This is not checked.

EXAMPLES:

Sage

sage: # needs sage.combinat
sage: L = posets.PentagonPoset()
sage: c = L.congruence([[0, 1]])
sage: I = L.quotient(c); I
Finite lattice containing 2 elements
sage: I.top()
(2, 3, 4)
sage: I = L.quotient(c, labels='lattice')
sage: I.top()
Finite lattice containing 3 elements

sage: # needs sage.combinat
sage: B3 = posets.BooleanLattice(3)
sage: c = B3.congruence([[0,1]])
sage: B2 = B3.quotient(c, labels='integer')
sage: B2.is_isomorphic(posets.BooleanLattice(2))
True

Python

>>> from sage.all import *
>>> # needs sage.combinat
>>> L = posets.PentagonPoset()
>>> c = L.congruence([[Integer(0), Integer(1)]])
>>> I = L.quotient(c); I
Finite lattice containing 2 elements
>>> I.top()
(2, 3, 4)
>>> I = L.quotient(c, labels='lattice')
>>> I.top()
Finite lattice containing 3 elements

>>> # needs sage.combinat
>>> B3 = posets.BooleanLattice(Integer(3))
>>> c = B3.congruence([[Integer(0),Integer(1)]])
>>> B2 = B3.quotient(c, labels='integer')
>>> B2.is_isomorphic(posets.BooleanLattice(Integer(2)))
True

See also

congruence()

skeleton()[source]¶

Return the skeleton of the lattice.

The lattice is expected to be pseudocomplemented.

The skeleton of a pseudocomplemented lattice \(L\), where \(^*\) is the pseudocomplementation operation, is the subposet induced by \(\{e^* \mid e \in L\}\). Actually this poset is a Boolean lattice.

EXAMPLES:

Sage

sage: D12 = posets.DivisorLattice(12)
sage: S = D12.skeleton(); S
Finite lattice containing 4 elements
sage: S.cover_relations()
[[1, 3], [1, 4], [3, 12], [4, 12]]

sage: T4 = posets.TamariLattice(4)
sage: T4.skeleton().is_isomorphic(posets.BooleanLattice(3))
True

Python

>>> from sage.all import *
>>> D12 = posets.DivisorLattice(Integer(12))
>>> S = D12.skeleton(); S
Finite lattice containing 4 elements
>>> S.cover_relations()
[[1, 3], [1, 4], [3, 12], [4, 12]]

>>> T4 = posets.TamariLattice(Integer(4))
>>> T4.skeleton().is_isomorphic(posets.BooleanLattice(Integer(3)))
True

subdirect_decomposition()[source]¶

Return the subdirect decomposition of the lattice.

The subdirect decomposition of a lattice \(L\) is the list of smaller lattices \(L_1, \ldots, L_n\) such that \(L\) is a sublattice of \(L_1 \times \ldots \times L_n\), none of \(L_i\) can be decomposed further and \(L\) is not a sublattice of any \(L_i\). (Except when the list has only one element, i.e. when the lattice is subdirectly irreducible.)

EXAMPLES:

Sage

sage: posets.ChainPoset(3).subdirect_decomposition()                        # needs sage.combinat
[Finite lattice containing 2 elements, Finite lattice containing 2 elements]

sage: # needs sage.combinat
sage: L = LatticePoset({1: [2, 4], 2: [3], 3: [6, 7], 4: [5, 7],
....:                   5: [9, 8], 6: [9], 7: [9], 8: [10], 9: [10]})
sage: Ldecomp = L.subdirect_decomposition()
sage: [fac.cardinality() for fac in Ldecomp]
[2, 5, 7]
sage: Ldecomp[1].is_isomorphic(posets.PentagonPoset())
True

Python

>>> from sage.all import *
>>> posets.ChainPoset(Integer(3)).subdirect_decomposition()                        # needs sage.combinat
[Finite lattice containing 2 elements, Finite lattice containing 2 elements]

>>> # needs sage.combinat
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(4)], Integer(2): [Integer(3)], Integer(3): [Integer(6), Integer(7)], Integer(4): [Integer(5), Integer(7)],
...                   Integer(5): [Integer(9), Integer(8)], Integer(6): [Integer(9)], Integer(7): [Integer(9)], Integer(8): [Integer(10)], Integer(9): [Integer(10)]})
>>> Ldecomp = L.subdirect_decomposition()
>>> [fac.cardinality() for fac in Ldecomp]
[2, 5, 7]
>>> Ldecomp[Integer(1)].is_isomorphic(posets.PentagonPoset())
True

sublattice(elms)[source]¶

Return the smallest sublattice containing elements on the given list.

INPUT:

elms – list of elements of the lattice

EXAMPLES:

Sage

sage: L = LatticePoset(([], [[1,2],[1,17],[1,8],[2,3],[2,22],[2,5],[2,7],[17,22],[17,13],[8,7],[8,13],[3,16],[3,9],[22,16],[22,18],[22,10],[5,18],[5,14],[7,9],[7,14],[7,10],[13,10],[16,6],[16,19],[9,19],[18,6],[18,33],[14,33],[10,19],[10,33],[6,4],[19,4],[33,4]]))
sage: L.sublattice([14, 13, 22]).list()
[1, 2, 8, 7, 14, 17, 13, 22, 10, 33]

sage: L = posets.BooleanLattice(3)
sage: L.sublattice([3,5,6,7])
Finite lattice containing 8 elements

Python

>>> from sage.all import *
>>> L = LatticePoset(([], [[Integer(1),Integer(2)],[Integer(1),Integer(17)],[Integer(1),Integer(8)],[Integer(2),Integer(3)],[Integer(2),Integer(22)],[Integer(2),Integer(5)],[Integer(2),Integer(7)],[Integer(17),Integer(22)],[Integer(17),Integer(13)],[Integer(8),Integer(7)],[Integer(8),Integer(13)],[Integer(3),Integer(16)],[Integer(3),Integer(9)],[Integer(22),Integer(16)],[Integer(22),Integer(18)],[Integer(22),Integer(10)],[Integer(5),Integer(18)],[Integer(5),Integer(14)],[Integer(7),Integer(9)],[Integer(7),Integer(14)],[Integer(7),Integer(10)],[Integer(13),Integer(10)],[Integer(16),Integer(6)],[Integer(16),Integer(19)],[Integer(9),Integer(19)],[Integer(18),Integer(6)],[Integer(18),Integer(33)],[Integer(14),Integer(33)],[Integer(10),Integer(19)],[Integer(10),Integer(33)],[Integer(6),Integer(4)],[Integer(19),Integer(4)],[Integer(33),Integer(4)]]))
>>> L.sublattice([Integer(14), Integer(13), Integer(22)]).list()
[1, 2, 8, 7, 14, 17, 13, 22, 10, 33]

>>> L = posets.BooleanLattice(Integer(3))
>>> L.sublattice([Integer(3),Integer(5),Integer(6),Integer(7)])
Finite lattice containing 8 elements

sublattices()[source]¶

Return all sublattices of the lattice.

EXAMPLES:

Sage

sage: L = LatticePoset({1: [2, 3, 4], 2:[5], 3:[5, 6], 4:[6],
....:                   5:[7], 6:[7]})
sage: sublats = L.sublattices(); len(sublats)
54
sage: sublats[3]
Finite lattice containing 4 elements
sage: sublats[3].list()
[1, 2, 3, 5]

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3), Integer(4)], Integer(2):[Integer(5)], Integer(3):[Integer(5), Integer(6)], Integer(4):[Integer(6)],
...                   Integer(5):[Integer(7)], Integer(6):[Integer(7)]})
>>> sublats = L.sublattices(); len(sublats)
54
>>> sublats[Integer(3)]
Finite lattice containing 4 elements
>>> sublats[Integer(3)].list()
[1, 2, 3, 5]

sublattices_lattice(labels='lattice')[source]¶

Return the lattice of sublattices.

Every element of the returned lattice is a sublattice and they are ordered by containment; that is, atoms are one-element lattices, coatoms are maximal sublattices of the original lattice and so on.

INPUT:

labels – string; can be one of the following:
- 'lattice' (default) elements of the lattice will be lattices that correspond to sublattices of the original lattice
- 'tuple' – elements are tuples of elements of the sublattices of the original lattice
- 'integer' – elements are plain integers

EXAMPLES:

Sage

sage: D4 = posets.DiamondPoset(4)
sage: sll = D4.sublattices_lattice(labels='tuple')
sage: sll.coatoms()  # = maximal sublattices of the original lattice
[(0, 1, 3), (0, 2, 3)]

sage: L = posets.DivisorLattice(12)
sage: sll = L.sublattices_lattice()
sage: L.is_dismantlable() == (len(sll.atoms()) == sll.rank())
True

Python

>>> from sage.all import *
>>> D4 = posets.DiamondPoset(Integer(4))
>>> sll = D4.sublattices_lattice(labels='tuple')
>>> sll.coatoms()  # = maximal sublattices of the original lattice
[(0, 1, 3), (0, 2, 3)]

>>> L = posets.DivisorLattice(Integer(12))
>>> sll = L.sublattices_lattice()
>>> L.is_dismantlable() == (len(sll.atoms()) == sll.rank())
True

vertical_composition(other, labels='pairs')[source]¶

Return the vertical composition of the lattice with other.

Let \(L\) and \(K\) be lattices and \(b_K\) the bottom element of \(K\). The vertical composition of \(L\) and \(K\) is the ordinal sum of \(L\) and \(K \setminus \{b_K\}\). Informally said this is lattices “glued” together with a common element.

Mathematically, it is only defined when \(L\) and \(K\) have no common element; here we force that by giving them different names in the resulting poset.

INPUT:

other – a lattice
labels – string (default: 'pairs'); can be one of the following:
- 'pairs' – each element v in this poset will be named (0, v) and each element u in other will be named (1, u) in the result
- 'integers' – the elements of the result will be relabeled with consecutive integers

EXAMPLES:

Sage

sage: L = LatticePoset({'a': ['b', 'c'], 'b': ['d'], 'c': ['d']})
sage: K = LatticePoset({'e': ['f', 'g'], 'f': ['h'], 'g': ['h']})
sage: M = L.vertical_composition(K)
sage: M.list()
[(0, 'a'), (0, 'b'), (0, 'c'), (0, 'd'), (1, 'f'), (1, 'g'), (1, 'h')]
sage: M.upper_covers((0, 'd'))
[(1, 'f'), (1, 'g')]

sage: C2 = posets.ChainPoset(2)
sage: M3 = posets.DiamondPoset(5)
sage: L = C2.vertical_composition(M3, labels='integers')
sage: L.cover_relations()
[[0, 1], [1, 2], [1, 3], [1, 4], [2, 5], [3, 5], [4, 5]]

Python

>>> from sage.all import *
>>> L = LatticePoset({'a': ['b', 'c'], 'b': ['d'], 'c': ['d']})
>>> K = LatticePoset({'e': ['f', 'g'], 'f': ['h'], 'g': ['h']})
>>> M = L.vertical_composition(K)
>>> M.list()
[(0, 'a'), (0, 'b'), (0, 'c'), (0, 'd'), (1, 'f'), (1, 'g'), (1, 'h')]
>>> M.upper_covers((Integer(0), 'd'))
[(1, 'f'), (1, 'g')]

>>> C2 = posets.ChainPoset(Integer(2))
>>> M3 = posets.DiamondPoset(Integer(5))
>>> L = C2.vertical_composition(M3, labels='integers')
>>> L.cover_relations()
[[0, 1], [1, 2], [1, 3], [1, 4], [2, 5], [3, 5], [4, 5]]

vertical_decomposition(elements_only=False)[source]¶

Return sublattices from the vertical decomposition of the lattice.

Let \(d_1, \ldots, d_n\) be elements (excluding the top and bottom elements) comparable to every element of the lattice. Let \(b\) be the bottom element and \(t\) be the top element. This function returns either a list \(d_1, \ldots, d_n\), or the list of intervals \([b, d_1], [d_1, d_2], \ldots, [d_{n-1}, d_n], [d_n, t]\) as lattices.

Informally said, this returns the lattice split into parts at every single-element “cutting point”.

INPUT:

elements_only – if True, return the list of decomposing elements as defined above; if False (the default), return the list of sublattices so that the lattice is a vertical composition of them.

EXAMPLES:

Number 6 is divided by 1, 2, and 3, and it divides 12, 18 and 36:

Sage

sage: L = LatticePoset( ([1, 2, 3, 6, 12, 18, 36],
....:     attrcall("divides")) )
sage: parts = L.vertical_decomposition()
sage: [lat.list() for lat in parts]
[[1, 2, 3, 6], [6, 12, 18, 36]]
sage: L.vertical_decomposition(elements_only=True)
[6]

Python

>>> from sage.all import *
>>> L = LatticePoset( ([Integer(1), Integer(2), Integer(3), Integer(6), Integer(12), Integer(18), Integer(36)],
...     attrcall("divides")) )
>>> parts = L.vertical_decomposition()
>>> [lat.list() for lat in parts]
[[1, 2, 3, 6], [6, 12, 18, 36]]
>>> L.vertical_decomposition(elements_only=True)
[6]

class sage.combinat.posets.lattices.FiniteMeetSemilattice(hasse_diagram, elements, category, facade, key)[source]¶

Bases: FinitePoset

Note

We assume that the argument passed to MeetSemilattice is the poset of a meet-semilattice (i.e. a poset with greatest lower bound for each pair of elements).

Element[source]¶: alias of MeetSemilatticeElement

atoms()[source]¶

Return the list atoms of this (semi)lattice.

An atom of a lattice is an element covering the bottom element.

EXAMPLES:

Sage

sage: L = posets.DivisorLattice(60)
sage: sorted(L.atoms())
[2, 3, 5]

Python

>>> from sage.all import *
>>> L = posets.DivisorLattice(Integer(60))
>>> sorted(L.atoms())
[2, 3, 5]

See also

Dual function: coatoms()

meet(x, y=None)[source]¶

Return the meet of given elements in the lattice.

INPUT:

x, y – two elements of the (semi)lattice OR
x – list or tuple of elements

EXAMPLES:

Sage

sage: D = posets.DiamondPoset(5)
sage: D.meet(1, 2)
0
sage: D.meet(1, 1)
1
sage: D.meet(1, 0)
0
sage: D.meet(1, 4)
1

Python

>>> from sage.all import *
>>> D = posets.DiamondPoset(Integer(5))
>>> D.meet(Integer(1), Integer(2))
0
>>> D.meet(Integer(1), Integer(1))
1
>>> D.meet(Integer(1), Integer(0))
0
>>> D.meet(Integer(1), Integer(4))
1

Using list of elements as an argument. Meet of empty list is the bottom element:

Sage

sage: B4=posets.BooleanLattice(4)
sage: B4.meet([3,5,6])
0
sage: B4.meet([])
15

Python

>>> from sage.all import *
>>> B4=posets.BooleanLattice(Integer(4))
>>> B4.meet([Integer(3),Integer(5),Integer(6)])
0
>>> B4.meet([])
15

For non-facade lattices operator * works for meet:

Sage

sage: L = posets.PentagonPoset(facade=False)
sage: L(1)*L(2)
0

Python

>>> from sage.all import *
>>> L = posets.PentagonPoset(facade=False)
>>> L(Integer(1))*L(Integer(2))
0

See also

Dual function: join()

meet_matrix()[source]¶

Return a matrix whose (i,j) entry is k, where self.linear_extension()[k] is the meet (greatest lower bound) of self.linear_extension()[i] and self.linear_extension()[j].

EXAMPLES:

Sage

sage: P = LatticePoset([[1,3,2],[4],[4,5,6],[6],[7],[7],[7],[]], facade = False)
sage: M = P.meet_matrix(); M
[0 0 0 0 0 0 0 0]
[0 1 0 1 0 0 0 1]
[0 0 2 2 2 0 2 2]
[0 1 2 3 2 0 2 3]
[0 0 2 2 4 0 2 4]
[0 0 0 0 0 5 5 5]
[0 0 2 2 2 5 6 6]
[0 1 2 3 4 5 6 7]
sage: M[P(4).vertex,P(3).vertex] == P(0).vertex
True
sage: M[P(5).vertex,P(2).vertex] == P(2).vertex
True
sage: M[P(5).vertex,P(2).vertex] == P(5).vertex
False

Python

>>> from sage.all import *
>>> P = LatticePoset([[Integer(1),Integer(3),Integer(2)],[Integer(4)],[Integer(4),Integer(5),Integer(6)],[Integer(6)],[Integer(7)],[Integer(7)],[Integer(7)],[]], facade = False)
>>> M = P.meet_matrix(); M
[0 0 0 0 0 0 0 0]
[0 1 0 1 0 0 0 1]
[0 0 2 2 2 0 2 2]
[0 1 2 3 2 0 2 3]
[0 0 2 2 4 0 2 4]
[0 0 0 0 0 5 5 5]
[0 0 2 2 2 5 6 6]
[0 1 2 3 4 5 6 7]
>>> M[P(Integer(4)).vertex,P(Integer(3)).vertex] == P(Integer(0)).vertex
True
>>> M[P(Integer(5)).vertex,P(Integer(2)).vertex] == P(Integer(2)).vertex
True
>>> M[P(Integer(5)).vertex,P(Integer(2)).vertex] == P(Integer(5)).vertex
False

pseudocomplement(element)[source]¶

Return the pseudocomplement of element, if it exists.

The (meet-)pseudocomplement is the greatest element whose meet with given element is the bottom element. I.e. in a meet-semilattice with bottom element \(\hat{0}\) the pseudocomplement of an element \(e\) is the element \(e^\star\) such that \(e \wedge e^\star = \hat{0}\) and \(e' \le e^\star\) if \(e \wedge e' = \hat{0}\).

See Wikipedia article Pseudocomplement.

INPUT:

element – an element of the lattice

OUTPUT:

An element of the lattice or None if the pseudocomplement does not exist.

EXAMPLES:

The pseudocomplement’s pseudocomplement is not always the original element:

Sage

sage: L = LatticePoset({1: [2, 3], 2: [4], 3: [5], 4: [6], 5: [6]})
sage: L.pseudocomplement(2)
5
sage: L.pseudocomplement(5)
4

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(1): [Integer(2), Integer(3)], Integer(2): [Integer(4)], Integer(3): [Integer(5)], Integer(4): [Integer(6)], Integer(5): [Integer(6)]})
>>> L.pseudocomplement(Integer(2))
5
>>> L.pseudocomplement(Integer(5))
4

An element can have complements but no pseudocomplement, or vice versa:

Sage

sage: L = LatticePoset({0: [1, 2], 1: [3, 4, 5], 2: [5], 3: [6],
....:                   4: [6], 5: [6]})
sage: L.complements(1), L.pseudocomplement(1)
([], 2)
sage: L.complements(2), L.pseudocomplement(2)
([3, 4], None)

Python

>>> from sage.all import *
>>> L = LatticePoset({Integer(0): [Integer(1), Integer(2)], Integer(1): [Integer(3), Integer(4), Integer(5)], Integer(2): [Integer(5)], Integer(3): [Integer(6)],
...                   Integer(4): [Integer(6)], Integer(5): [Integer(6)]})
>>> L.complements(Integer(1)), L.pseudocomplement(Integer(1))
([], 2)
>>> L.complements(Integer(2)), L.pseudocomplement(Integer(2))
([3, 4], None)

See also

is_pseudocomplemented()

subjoinsemilattice(elms)[source]¶

Return the smallest join-subsemilattice containing elements on the given list.

INPUT:

elms – list of elements of the lattice

EXAMPLES:

Sage

sage: L = posets.DivisorLattice(1000)
sage: L_ = L.subjoinsemilattice([2, 25, 125]); L_
Finite join-semilattice containing 5 elements
sage: sorted(L_.list())
[2, 25, 50, 125, 250]

Python

>>> from sage.all import *
>>> L = posets.DivisorLattice(Integer(1000))
>>> L_ = L.subjoinsemilattice([Integer(2), Integer(25), Integer(125)]); L_
Finite join-semilattice containing 5 elements
>>> sorted(L_.list())
[2, 25, 50, 125, 250]

See also

Dual function: submeetsemilattice()

submeetsemilattice(elms)[source]¶

Return the smallest meet-subsemilattice containing elements on the given list.

INPUT:

elms – list of elements of the lattice

EXAMPLES:

Sage

sage: L = posets.DivisorLattice(1000)
sage: L_ = L.submeetsemilattice([200, 250, 125]); L_
Finite meet-semilattice containing 5 elements
sage: L_.list()
[25, 50, 200, 125, 250]

Python

>>> from sage.all import *
>>> L = posets.DivisorLattice(Integer(1000))
>>> L_ = L.submeetsemilattice([Integer(200), Integer(250), Integer(125)]); L_
Finite meet-semilattice containing 5 elements
>>> L_.list()
[25, 50, 200, 125, 250]

See also

Dual function: subjoinsemilattice()

sage.combinat.posets.lattices.JoinSemilattice(data=None, *args, **options)[source]¶

Construct a join semi-lattice from various forms of input data.

INPUT:

data, *args, **options – data and options that will be passed down to Poset() to construct a poset that is also a join semilattice

EXAMPLES:

Using data that defines a poset:

Sage

sage: JoinSemilattice([[1,2],[3],[3]])
Finite join-semilattice containing 3 elements

sage: JoinSemilattice([[1,2],[3],[3]], cover_relations = True)
Finite join-semilattice containing 3 elements

Python

>>> from sage.all import *
>>> JoinSemilattice([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]])
Finite join-semilattice containing 3 elements

>>> JoinSemilattice([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]], cover_relations = True)
Finite join-semilattice containing 3 elements

Using a previously constructed poset:

Sage

sage: P = Poset([[1,2],[3],[3]])
sage: J = JoinSemilattice(P); J
Finite join-semilattice containing 3 elements
sage: type(J)
<class 'sage.combinat.posets.lattices.FiniteJoinSemilattice_with_category'>

Python

>>> from sage.all import *
>>> P = Poset([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]])
>>> J = JoinSemilattice(P); J
Finite join-semilattice containing 3 elements
>>> type(J)
<class 'sage.combinat.posets.lattices.FiniteJoinSemilattice_with_category'>

If the data is not a lattice, then an error is raised:

Sage

sage: JoinSemilattice({'a': ['b', 'c'], 'b': ['d', 'e'],
....:                  'c': ['d', 'e'], 'd': ['f'], 'e': ['f']})
Traceback (most recent call last):
...
LatticeError: no join for b and c

Python

>>> from sage.all import *
>>> JoinSemilattice({'a': ['b', 'c'], 'b': ['d', 'e'],
...                  'c': ['d', 'e'], 'd': ['f'], 'e': ['f']})
Traceback (most recent call last):
...
LatticeError: no join for b and c

sage.combinat.posets.lattices.LatticePoset(data=None, *args, **options)[source]¶

Construct a lattice from various forms of input data.

INPUT:

data, *args, **options – data and options that will be passed down to Poset() to construct a poset that is also a lattice.

OUTPUT: an instance of FiniteLatticePoset

See also

Posets, FiniteLatticePosets, JoinSemiLattice(), MeetSemiLattice()

EXAMPLES:

Using data that defines a poset:

Sage

sage: LatticePoset([[1,2],[3],[3]])
Finite lattice containing 3 elements

sage: LatticePoset([[1,2],[3],[3]], cover_relations = True)
Finite lattice containing 3 elements

Python

>>> from sage.all import *
>>> LatticePoset([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]])
Finite lattice containing 3 elements

>>> LatticePoset([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]], cover_relations = True)
Finite lattice containing 3 elements

Using a previously constructed poset:

Sage

sage: P = Poset([[1,2],[3],[3]])
sage: L = LatticePoset(P); L
Finite lattice containing 3 elements
sage: type(L)
<class 'sage.combinat.posets.lattices.FiniteLatticePoset_with_category'>

Python

>>> from sage.all import *
>>> P = Poset([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]])
>>> L = LatticePoset(P); L
Finite lattice containing 3 elements
>>> type(L)
<class 'sage.combinat.posets.lattices.FiniteLatticePoset_with_category'>

If the data is not a lattice, then an error is raised:

Sage

sage: elms = [1,2,3,4,5,6,7]
sage: rels = [[1,2],[3,4],[4,5],[2,5]]
sage: LatticePoset((elms, rels))
Traceback (most recent call last):
...
ValueError: not a meet-semilattice: no bottom element

Python

>>> from sage.all import *
>>> elms = [Integer(1),Integer(2),Integer(3),Integer(4),Integer(5),Integer(6),Integer(7)]
>>> rels = [[Integer(1),Integer(2)],[Integer(3),Integer(4)],[Integer(4),Integer(5)],[Integer(2),Integer(5)]]
>>> LatticePoset((elms, rels))
Traceback (most recent call last):
...
ValueError: not a meet-semilattice: no bottom element

Creating a facade lattice:

Sage

sage: L = LatticePoset([[1,2],[3],[3]], facade = True)
sage: L.category()
Category of facade finite enumerated lattice posets
sage: parent(L[0])
Integer Ring
sage: TestSuite(L).run(skip = ['_test_an_element']) # is_parent_of is not yet implemented

Python

>>> from sage.all import *
>>> L = LatticePoset([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]], facade = True)
>>> L.category()
Category of facade finite enumerated lattice posets
>>> parent(L[Integer(0)])
Integer Ring
>>> TestSuite(L).run(skip = ['_test_an_element']) # is_parent_of is not yet implemented

sage.combinat.posets.lattices.MeetSemilattice(data=None, *args, **options)[source]¶

Construct a meet semi-lattice from various forms of input data.

INPUT:

data, *args, **options – data and options that will be passed down to Poset() to construct a poset that is also a meet semilattice.

EXAMPLES:

Using data that defines a poset:

Sage

sage: MeetSemilattice([[1,2],[3],[3]])
Finite meet-semilattice containing 3 elements

sage: MeetSemilattice([[1,2],[3],[3]], cover_relations = True)
Finite meet-semilattice containing 3 elements

Python

>>> from sage.all import *
>>> MeetSemilattice([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]])
Finite meet-semilattice containing 3 elements

>>> MeetSemilattice([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]], cover_relations = True)
Finite meet-semilattice containing 3 elements

Using a previously constructed poset:

Sage

sage: P = Poset([[1,2],[3],[3]])
sage: L = MeetSemilattice(P); L
Finite meet-semilattice containing 3 elements
sage: type(L)
<class 'sage.combinat.posets.lattices.FiniteMeetSemilattice_with_category'>

Python

>>> from sage.all import *
>>> P = Poset([[Integer(1),Integer(2)],[Integer(3)],[Integer(3)]])
>>> L = MeetSemilattice(P); L
Finite meet-semilattice containing 3 elements
>>> type(L)
<class 'sage.combinat.posets.lattices.FiniteMeetSemilattice_with_category'>

If the data is not a lattice, then an error is raised:

Sage

sage: MeetSemilattice({'a': ['b', 'c'], 'b': ['d', 'e'],
....:                  'c': ['d', 'e'], 'd': ['f'], 'e': ['f']})
Traceback (most recent call last):
...
LatticeError: no meet for e and d

Python

>>> from sage.all import *
>>> MeetSemilattice({'a': ['b', 'c'], 'b': ['d', 'e'],
...                  'c': ['d', 'e'], 'd': ['f'], 'e': ['f']})
Traceback (most recent call last):
...
LatticeError: no meet for e and d